- (Обновлено: ) Елена Камская
Мы подготовили для вас перевод доклада Яндекса о его новой разработке SupervisedNestedPageRank. Тем, у кого нет научной степени по математике, понять его будет довольно-таки сложно. Поэтому перевод мы дополнили разъяснениями Ильи Зябрева и Олега Пожаркова, они более простым языком объясняют, в чем заключается разработка Яндекса.
Доклад, который Яндекс представил на конференции CIKM 2014, для SEO-специалистов без ученой степени по математике будет сложным для восприятия. Поэтому мы дополнили его перевод разъяснениями Ильи Зябрева и Олега Пожаркова. Они проливают свет на представленную сотрудниками Яндекса разработку SupervisedNestedPageRank.
Maxim Zhukovskiy Gleb Gusev Pavel Serdyukov
16 Leo Tolstoy St., Moscow, 119021 Russia
{zhukmax, gleb57, pavser}@yandex-team.ru
Аннотация
Ранжирование на основе графов широко используется во многих областях, таких, как интернет-поиск и социальные исследования. Одни из первых методов ранжирования с использованием графов (например, PageRank и HITS) применяли для вычисления оценок исключительно их (графов) структуры.
Разработанные недавно методы, такие, как Semi-Supervised Page-Rank, используют и структуру графа, и внешние данные, связанные с его узлами и ребрами. Такие алгоритмы основаны на моделях случайных блужданий с учетом исходных весов узлов и ребер, которые зависят только от их свойств. В таких моделях исходные веса вершин и ребер определяются только их собственными характеристиками, однако эти величины могут также быть связаны со свойствами их «соседей». Данная статья посвящена задаче «взвешивания» узлов и ребер на основе этой идеи и ее реализации в виде общей модели ранжирования, а также эффективному алгоритму настройки ее параметров.
Основные определения: алгоритмы, экспериментальное исследование.
Ключевые слова: вес страницы, PageRank, случайные блуждания, новизна, свойства контента, интернет поиск, обучение
1. ВВЕДЕНИЕ
В настоящее время различные графы, такие, как веб-граф, граф переходов пользователя, граф «запрос-выдача», социальные сети и другие множества со значительным объемом информации на узлах, доступны для больших информационных систем. В некоторых из них, например, поисковых системах или социальных сетевых сервисах, ранжирование на базе графов всегда было одной из ключевых технологий. Наиболее распространенные из методов основаны на моделях случайного блуждания: PageRank [17], HITS [11], и различные их разновидности (см. [9, 18]). Например, алгоритм PageRank оценивает вес узла p как его стационарную вероятность в распределении марковского процесса, который моделирует случайное блуждание по графу (первоначально алгоритм использовался на веб-графах). Случайное блуждание может быть определено в виде совокупности начальных вероятностей и вероятностей переходов. В исходном алгоритме PageRank начальные вероятности для всех узлов равны, так же, как и равны все вероятности перехода для конечных узлов. А в более свежих модификациях алгоритма эти вероятности могут существенно зависеть от свойств узлов и ребер между ними. Например, если узлы — это документы веб-графа [17] или графа переходов пользователя [14], его вершины и ребра могут содержать некоторые метаданные, включающие статистику о взаимодействиях пользователей со страницами (число или средняя продолжительность посещений страницы пользователями или число переходов между ними), их языковые модели или истории их изменений. Такая информация определяет свойства узлов и ребер и может использоваться для более точного «взвешивания» страниц по сравнению с методами, основанными исключительно на геометрической структуре графа.
Существует множество работ, посвященных задаче выбора вышеупомянутых свойств узлов и ребер для ранжирования графа. Модели, описанные в ранних исследованиях [5, 13, 18], используют свойства вершин и ребер «жестким» способом, не допуская их настройку для частных вариантов использования. Авторы поздних работ [5, 6, 8, 9] предлагают более гибкие системы ранжирования, которые могут использовать одни и те же свойства различными способами в рамках некоторой параметрической модели. Другими словами, веса страниц (соответствующие начальным вероятностям) и веса ребер (соответствующие вероятностям переходов) определяются в виде параметрических функций от их свойств, с учетом их значимости, управляя, таким образом, характером случайного блуждания.
Основная проблема состоит в том, чтобы реализовать вышеупомянутые параметры в виде управляемых настроек. Старые методы оптимизации [7] работают только на линейных моделях PageRank, когда веса вершин и ребер представляют собой линейные комбинации их свойств, а в качестве параметров используются числовые коэффициенты. При этом вес некоторого узла (или ребра) зависит только от его особенностей и не зависит от свойств смежных с ним объектов. Данное обстоятельство создает ряд существенных ограничений.
Во-первых, во многих случаях некоторые свойства страницы распределены неравномерно, что может иногда приводить к непропорциональной разнице в весах соседних узлов. Этот эффект плохо согласуется с предположением о том, что сосед вершины с высоким весом, вероятно, будет также иметь высокий вес, по крайней мере для методов ранжирования на основе графов. Например, у старого документа может быть множество недавно созданных «соседей». Соответственно его возраст будет значительно выше, чем у новых страниц, и если вес документа зависит от даты создания, то необходимо «сгладить» соответствующее свойство со свойствами соседей.
Во-вторых, некоторые метаданные, необходимые для расчетов свойств узлов и ребер, могут редко встречаться или быть неточными, чтобы им доверять. Например, можно упустить любую информацию о кликах для некоторых страниц, даже если они отображаются в SERP, но на недостаточно высоких позициях, чтобы быть замеченными пользователями. Такие ситуации также не учитываются старыми методами оптимизации алгоритмов ранжирования на базе графов.
В-третьих, если значения свойств зашумлены, то это может вызвать значительные колебания весов, при перемещении от узла к его «соседу». Например, нет никакого смысла вычислять среднее число просмотров страницы, которую посетил несколько раз только один пользователь, потому что это приведет к очень неточной оценке.
В этой статье мы предлагаем новый метод под названием Supervised Nested PageRank (SNP) для обучения модели ранжирования страниц, которая устраняет вышеупомянутые недостатки. Подобно линейным моделям на основе PageRank, наш метод основан на параметрическом обучении первичной случайной модели блуждания, которая определяется весами узлов и ребер. При этом вес объекта (вершины или ребра) определяется не только его собственными свойствами, но и свойствами его «соседей», и эта зависимость позволяет сглаживать полученные значения вдоль всего графа. Исходные веса узлов и ребер определяются стационарными распределениями двух вторичных марковских процессов, которые строятся на исходном графе при помощи одних и тех же уравнений, но с независимыми наборами параметров. Веса вершин, которые определяют начальные вероятности первичного процесса Маркова, равны соответствующим стационарным вероятностям, полученным для первого из двух вложенных (вторичных) марковских процессов. Веса ребер, которые определяют вероятности переходов первичного марковского процесса, равны стационарным вероятностям конечных узлов, полученных для второго вложенного процесса. Таким образом, вторичные случайные блуждания распределяют значения свойств узлов и ребер по «поверхности» графа, что позволяет избежать вышеописанных нежелательных эффектов. Мы называем процессы такого типа вложенными.
Система ранжирования на базе SNP зависит от вектора параметров. Мы разработали новый градиентный метод оптимизации для настройки параметров модели. Он основан на вычислении производных стационарных вероятностей модели относительно ее параметров. Наш метод оптимизации довольно эффективен: его вычислительная сложность равна количеству шагов градиентного спуска, умноженному на сложность алгоритма PageRank. Метод может использоваться для более широкого класса задач оптимизации с гладкими функциями стационарных вероятностей. Насколько нам известно, мы первые, кто представляет алгоритм формирования оптимальных параметров для вложенных процессов, используемых для ранжирования документов.
Основные тезисы данной статьи следующие:
— Представлен новый алгоритм SNP, основанный на случайном блуждании, определяемом весами узлов и ребер, которые в свою очередь определяются случайными блужданиями на базе их свойств. Этот алгоритм позволяет избавиться от некоторых ограничений подходов на базе линейных моделей ранжирования (PageRank) и позволяет максимизировать качество «взвешивания» страниц.
— Представлен алгоритм оптимизации параметров SNP относительно целевой функции, определяющей качество ранжирования. В частности, проведено исследование нового алгоритма вычисления производных стационарного распределения марковского процесса относительно его параметров. Этот алгоритм может также применяться для эффективной оптимизации линейного взвешивания.
— Произведена оценка нашего алгоритма на базе ссылочного графа с двумя различными наборами свойств узлов и ребер и показано, что наш подход дает более высокое качество, чем передовой метод SSP [7]. Также проведены эксперименты, показывающие, что SNP более устойчив к разреженности значений свойств узлов и ребер по сравнению с SSP.
Нижеследующая часть статьи организована следующим образом.
Раздел 2 содержит обзор ранжирующих алгоритмов графов, основанных на случайных блужданиях, матрица перехода которых зависит от свойств узлов и ребер.
В Разделе 3 описывается алгоритм Supervised Nest PageRank.
В Разделе 4 представлен метод оптимизации, который используется для настройки параметров нашего алгоритма.
Раздел 5 содержит описания графов, на базе которых проводились эксперименты, свойства их узлов и ребер, и целевые функции, используемые для сравнения методов.
Результаты экспериментов представлены в Разделе 6.
В Разделе 7 подводятся итоги наших исследований, обсуждается их возможное использование и направления будущих работ.
2. ОБЗОР АНАЛОГИЧНЫХ ПОДХОДОВ
Основанные на графе методы ранжирования, такие, как PageRank, могут быть параметризированы различными способами. Проблема взвешивания узлов и ребер для лучшего ранжирования страниц возникает на всем множестве вариантов использования графов: ранжирование веб-страниц [5, 7, 9, 13, 17, 18], поиск научных статей и идентификация сущностей [12], поиск по образцу [15], предсказание связей в социальных сетях [1]. Для каждой из указанных прикладных областей существует некоторая информация об узлах или ребрах, которая не учитывается в исходном алгоритме PageRank [17].
Было разработано несколько методов, которые расширяют базовую модель PageRank [7, 9, 18, 21]. В этих работах авторы определяют параметрические модели, где выбор пользователя о переходе к странице непосредственно или через ссылку зависит от их (страницы и ссылки) весов. Однако авторы первой из подобных моделей (например, [9, 18]) не вводят теоретического обоснования метода оптимизации параметров таких случайных блужданий. В [1] Бэкстрем и др. разработали модификацию PageRank под названием Управляемое Случайное Блуждание для задачи предсказания связей. В этой работе только веса ребер зависят от метаданных. Гао и др. [7] обобщили вышеуказанные методы, введя структуру под названием Semi-Supervised PageRank (SSP). Стоит отметить, что множество классических методов ранжирования на базе графа (кроме уже перечисленных), LiftHITS [4], NetRank [3], Laplacian [22]), можно представить в виде частных случаев SSP.
Грубо говоря, веса узлов и ребер все вышеупомянутые алгоритмы рассматривают в виде определенных линейных комбинаций некоторых их свойств. Также всегда считалось, что вес узла (или ребра) зависит только от его свойств. Ограничения, которые накладывает такой подход, были описаны в Разделе 1. В отличие от этих методов, наш основан на идее, что веса узлов и ребер должны учитывать свойства смежных с ними объектов, что позволяет «сглаживать» их вдоль всего графа.
Частный случай модели вложенного PageRank, которая рассмотрена в данной статье, был ранее описан Дэем и др. [5] и позже был расширен в [26]. Эти публикации были посвящены проблеме чувствительности алгоритма ранжирования веб-графа к возрасту его вершин. Для ее решения авторы разработали случайные блуждания, определяемые весами, которые по сути являются «свежестью» узлов в веб-графе. В этих подходах вес узла зависит от его собственных свойств, а также от свойств его соседей. Однако данные модели не обеспечены методами оптимизации для настройки их многочисленных параметров. Также в посвященных им статьях не были оценены преимущества, которые дает их сложная структура. Наше же исследование представляет собой попытку обобщить вложенные модели, изучить их преимущества перед более простым, но все же эффективным подходом SSP, и «усилить» их методом оптимизации основных параметров случайных блужданий.
BrowseRank [13] – эффективный метод ранжирования страниц, который использует граф пользовательских просмотров. Основанный на непрерывных марковских процессах, BrowseRank может быть представлен как частный случай SSP со всеми его недостатками (если мы сводим его к дискретному случаю, как предложено в статье). В [27], авторы описывают Fresh BrowseRank, использующий вложенные процессы на графе просмотров с учетом информации о новизне узлов. К сожалению, в этой короткой статье не описывается общая модель, которую можно использовать для широкого класса подобных задач, и не дается теоретического обоснования их собственной модели. При этом SNP, предложенный в настоящей статье, является общей и теоретически обоснованной моделью, которая может быть также использована для непрерывных марковских процессов. Кроме того, авторы [27], не представили какого-либо метода оптимизации параметров, которая сделала бы их модель практически реализуемой (т.е. не был представлен алгоритм вычисления производных), в то время как данный метод является одним из самых значимых преимуществ нашей технологии.
3. СУТЬ МЕТОДА
В этом разделе вводится метод ранжирования узлов графа. Пусть R – множество задач ранжирования, и для каждой задачи q {1,2,…R} мы должны определить ранги всех узлов. Например, если мы рассматриваем задачу запросного ранжирования веб-страниц, тогда запрос пользователя можно считать задачей как таковой. Алгоритм ранжирования на основе случайного блуждания использует в качестве входных данных свойства узлов и ребер, которые могут зависеть от условий задачи. Кроме них на выход алгоритма влияют также и его параметры, которые используются для его настройки и, при этом, не зависят от задачи. Ниже представлен алгоритм, определяющий значения параметров вложенных случайных блужданий, которые оптимизируют граф для всех задач в среднем.
3.1 Semi-supervised PageRank
Пусть q {1…, R} — задачи ранжирования. Определим граф как кортеж ![]() , где V — множество n узлов, E — множество ребер,
, где V — множество n узлов, E — множество ребер, ![]() множество векторов — свойств узлов (Viq — вектор свойств узла i размерностью l),
множество векторов — свойств узлов (Viq — вектор свойств узла i размерностью l), ![]() множество векторов — свойств ребер (Eqij — вектор свойств ребра i→j размерностью h). Полагаем, что Eij = 0, если i→j не существует. Например, для информационного поиска: если ссылка является внешней, то это может быть значимым свойством соответствующего ребра. Аналогично вес страницы, который определяется ее релевантностью, может быть значимым свойством соответствующего узла.
множество векторов — свойств ребер (Eqij — вектор свойств ребра i→j размерностью h). Полагаем, что Eij = 0, если i→j не существует. Например, для информационного поиска: если ссылка является внешней, то это может быть значимым свойством соответствующего ребра. Аналогично вес страницы, который определяется ее релевантностью, может быть значимым свойством соответствующего узла.
Пусть X, Y — наборы параметров и ![]() ,
, ![]() : положительные вещественные функции, которые определяют веса в рамках задачи q следующим образом. Для фиксированных значений параметров
: положительные вещественные функции, которые определяют веса в рамках задачи q следующим образом. Для фиксированных значений параметров ![]() , веса узла i из V и ребра i→j из E определяются как
, веса узла i из V и ребра i→j из E определяются как ![]() и
и ![]() соответственно. При этом значения функции f (и функции g) зависят от свойств узлов и ребер, а также Vq, Eq. Кроме того, значения функции f (или функции g) для узла i (ребра i→j) может зависеть не только от i-го элемента Vq (от элемента Eq для ребра i→j).
соответственно. При этом значения функции f (и функции g) зависят от свойств узлов и ребер, а также Vq, Eq. Кроме того, значения функции f (или функции g) для узла i (ребра i→j) может зависеть не только от i-го элемента Vq (от элемента Eq для ребра i→j).
Semi-Supervised PageRank (SSP, [7]) определяется стационарным распределением, полученным на основе случайного блуждания по вершинам графа, которое определено для рассматриваемой задачи q следующим образом. Пользователь переходит от одного узла к другому за один шаг. Находясь в узле i, он решает перейти к любому другому узлу с вероятностью α или исходящему ребру с вероятностью 1-α. Если пользователь идет по ребру, то именно i→j выбирается с вероятностью перехода
![]() (1)
(1)
Если пользователь выбирает случайный узел, то j выбирается с начальной вероятностью
![]() (2)
(2)
N-мерный вектор ![]() — это стационарное распределение марковского процесса (см. [16]). Таким образом, данное распределение представляет собой решение следующей системы уравнений:
— это стационарное распределение марковского процесса (см. [16]). Таким образом, данное распределение представляет собой решение следующей системы уравнений:
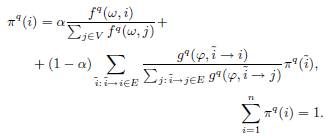 (3)
(3)
Отметим, что это выражение определяет стационарное распределение, при условии, что узлы с суммарным количеством исходящих ребер, равным нулю, отсутствуют (см. [8]). Если данное условие не выполняется, необходимо добавить в граф G дополнительный (виртуальный) узел, смежный со всеми другими узлами графа, как это было предположено в [6]. Значения вероятностей стационарного распределения можно рассмотреть как оценки узлов G, которые являются решением задачи q (см., например, [17, 7]). Предположим, что для каждой задачи q {1…, R} имеется ![]() -размерный вектор оценок, выставленных асессорами некоторым
-размерный вектор оценок, выставленных асессорами некоторым ![]() узлам в соответствии с их релевантностью задаче q. Совокупность этих векторов формирует репрезентативное подмножество
узлам в соответствии с их релевантностью задаче q. Совокупность этих векторов формирует репрезентативное подмножество ![]() . В частности, если узлы графа — веб-страницы, то R можно рассматривать как множество запросов. Пусть
. В частности, если узлы графа — веб-страницы, то R можно рассматривать как множество запросов. Пусть ![]() — функция невязки двух векторов
— функция невязки двух векторов ![]() и
и ![]() (например, ранговое расстояние или оценка качества поиска, если эти векторы представляют собой субъективное и идеальное ранжирование соответственно). Рассмотрим среднюю невязку
(например, ранговое расстояние или оценка качества поиска, если эти векторы представляют собой субъективное и идеальное ранжирование соответственно). Рассмотрим среднюю невязку
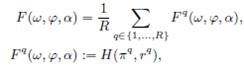 (4)
(4)
как объект минимизации так, как это было сделано в [15]. Задача оптимизации
![]()
может быть решена при помощи градиентных методов (см. Раздел 5.1).
Тип задач q зависит от природы рассматриваемого графа и задачи ранжирования. Например, частная задача предсказания наличия связи [1] состоит в том, чтобы оценить вероятность, с которой некоторые узлы будут связаны с данным в будущем. В такой постановке свойство, определяемое задачей, это бинарная функция, которая идентифицирует узел q. Задачей в ранжировании документов является пользовательский запрос, а свойство узла — оценка релевантности на основе BM25. Когда результат алгоритма не зависит от задачи q, линейную комбинацию с зависимым ранжированием bq можно представить в виде [7, 26, 27] (см. Раздел 5.1):
![]() (5)
(5)
Т.к. метод SSP [7] использует только свойства отдельных узлов и ребер, чтобы определить вероятности перехода через них, то их веса не зависят от «контекста» задачи. Поэтому во внимание не принимается тот факт, что свойства объектов могут в некоторой степени определяться свойствами смежных с ними узлов и ребер. В следующем разделе будет описано, как использовать данное обстоятельство при настройке модели случайного блуждания, используемой для ранжирования.
3.2 Взвешивание узлов и ребер
Здесь мы обсудим возможные методы представления весов ![]() , используемых в Уравнениях 1, 2, которые определяют начальные вероятности и вероятности переходов соответственно. Для начала продолжим рассмотрение метода SSP [1, 2, 9] и затем введем наш новый метод, который является его улучшением.
, используемых в Уравнениях 1, 2, которые определяют начальные вероятности и вероятности переходов соответственно. Для начала продолжим рассмотрение метода SSP [1, 2, 9] и затем введем наш новый метод, который является его улучшением.
В SSP множества параметров ![]() соответствуют множествам свойств вершин и ребер. Другими словами, веса определяются уравнениями:
соответствуют множествам свойств вершин и ребер. Другими словами, веса определяются уравнениями:
![]() (6)
(6)
Эти уравнения, таким образом, определяют в узком смысле линейную зависимость веса узла (ребра) от его вектора свойств. Также стоит отметить, что вес, определенный таким образом, зависит только от свойств рассматриваемого узла (ребра). Данный подход можно обобщить, как это было сделано в [1], рассматривая веса
![]()
где ![]() — некоторые монотонные функции (в частном случае
— некоторые монотонные функции (в частном случае ![]() мы получаем Уравнение 6).
мы получаем Уравнение 6).
Наш метод основан на следующем предположении. В большинстве задач, включая и рассматриваемые в Разделе 5, назначение весов состоит в том, чтобы определить начальные значения, которые оценивают некоторое качество узла или силу ребра между узлами. Логично предположить, что данные начальные оценки весов могут также зависеть от оценок соседей. При этом узел или ребро может получить часть весов своих соседей на основании того, что смежные с более весомым объектом элементы графа могут также иметь высокий вес, и наоборот. Сглаживание начального веса узла (ребра) начальными весами его соседей может быть также выполнено при помощи случайного блуждания. Таким образом, мы определяем финальные веса объекта как стационарное распределение марковского случайного блуждания, инициализированного на основе начальных весов, которые зависят только от свойств узла (ребра). Т.е. мы получаем двухэтапное случайное блуждание, где стационарные распределения вложенных блужданий (первый этап) представляют собой начальные веса внешнего блуждания (второй стадии).
Частные случаи таких вложенных процессов Маркова недавно описывались в [5, 26, 27]. В данной статье представлены общие положения для таких процессов и их приложений.
В частности мы предлагаем определять веса вершин и ребер, которые представлены в Уравнении 3, для получения стационарного распределения π уравнениями:
![]() (7)
(7)
где ![]() — стационарные распределения случайных марковских процессов, которые определяют начальные веса вершин (ребер). Отметим, что второе уравнение выражает зависимость только от конечного узла ребра i→j. Это соответствует распространенному методу взвешивания ребер значениями весов их конечных вершин. В рамках нашей работы можно использовать, скажем, линейную комбинацию
— стационарные распределения случайных марковских процессов, которые определяют начальные веса вершин (ребер). Отметим, что второе уравнение выражает зависимость только от конечного узла ребра i→j. Это соответствует распространенному методу взвешивания ребер значениями весов их конечных вершин. В рамках нашей работы можно использовать, скажем, линейную комбинацию ![]() . Рассмотрим случай
. Рассмотрим случай ![]() по следующим двум причинам. Во-первых, этот случай — обобщение моделей из [5, 18, 26, 27], означающий, что случайный пользователь двигается в направлении более «тяжелых» узлов так, что вес ребер может быть оценен значимостью их конечных вершин. Во-вторых, не стоит увеличивать сложность алгоритма в отсутствии потребности в дополнительных параметрах.
по следующим двум причинам. Во-первых, этот случай — обобщение моделей из [5, 18, 26, 27], означающий, что случайный пользователь двигается в направлении более «тяжелых» узлов так, что вес ребер может быть оценен значимостью их конечных вершин. Во-вторых, не стоит увеличивать сложность алгоритма в отсутствии потребности в дополнительных параметрах.
Стационарное распределение ![]() определяется уравнением, аналогичным Уравнению 3. На этот раз мы предлагаем использовать алгоритм взвешивания, предложенный в SSP, где вершины и ребра оцениваются на основе Уравнения 6. Однако назначения G1 и G2 отличаются, так как они определяют веса f и g, которые играют различные роли в Уравнениях 3, 7. Поэтому оптимальные значения параметров
определяется уравнением, аналогичным Уравнению 3. На этот раз мы предлагаем использовать алгоритм взвешивания, предложенный в SSP, где вершины и ребра оцениваются на основе Уравнения 6. Однако назначения G1 и G2 отличаются, так как они определяют веса f и g, которые играют различные роли в Уравнениях 3, 7. Поэтому оптимальные значения параметров ![]() могут отличаться, поскольку мы используем их для определения G1 и G2. Отметим, что нахождение оптимальных значений данных параметров является нетривиальной задачей: они определяют случайные блуждания, стационарные распределения которых влияют на веса f, g, которые в свою очередь определяют первичный марковский процесс, и его стационарное распределение, которое должно минимизировать функцию F. Каждый из вложенных марковских процессов описывается уравнением:
могут отличаться, поскольку мы используем их для определения G1 и G2. Отметим, что нахождение оптимальных значений данных параметров является нетривиальной задачей: они определяют случайные блуждания, стационарные распределения которых влияют на веса f, g, которые в свою очередь определяют первичный марковский процесс, и его стационарное распределение, которое должно минимизировать функцию F. Каждый из вложенных марковских процессов описывается уравнением:
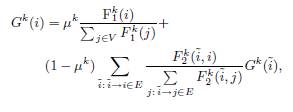 (8)
(8)
где ![]() являются коэффициентами затухания случайных блужданий, а
являются коэффициентами затухания случайных блужданий, а ![]() — начальные веса вершин и ребер соответственно. Это означает, что начальные вероятности этих марковских процессов пропорциональны
— начальные веса вершин и ребер соответственно. Это означает, что начальные вероятности этих марковских процессов пропорциональны![]() , а вероятности переходов пропорциональны
, а вероятности переходов пропорциональны ![]() . Как говорилось ранее, веса
. Как говорилось ранее, веса ![]() определяются уравнениями, аналогичными Уравнению 6:
определяются уравнениями, аналогичными Уравнению 6:
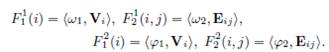 (9)
(9)
В отличие от SSP, мы, таким образом, ввели f и g, которые зависят и от свойств вершин, и от свойств ребер согласно Уравнениям 7–9, что является целесообразным, так как эти веса — результат процесса случайного блуждания и, следовательно, могут быть определены полным набором его параметров. Таким образом, в нашем методе взвешивания вектор параметров ![]() (вектор
(вектор ![]() ), который определяет весовую функцию f (функцию g), состоит из двух частей
), который определяет весовую функцию f (функцию g), состоит из двух частей ![]() размерностью l и h, где первая часть соответствует свойствам узлов, а вторая — ребер, и включает дополнительные параметры
размерностью l и h, где первая часть соответствует свойствам узлов, а вторая — ребер, и включает дополнительные параметры ![]() (коэффициенты затухания):
(коэффициенты затухания):
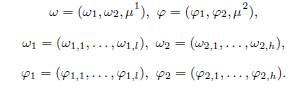
Подчеркнем, что компоненты этих векторов и компоненты векторов ![]() должны быть неотрицательными для того, чтобы получить неотрицательные веса
должны быть неотрицательными для того, чтобы получить неотрицательные веса ![]() , определяющие вероятности переходов и начальные вероятности марковских случайных процессов. В Разделе 4 будет рассмотрен метод обучения параметров ω и φ. Предположим, что для каждого узла
, определяющие вероятности переходов и начальные вероятности марковских случайных процессов. В Разделе 4 будет рассмотрен метод обучения параметров ω и φ. Предположим, что для каждого узла![]() сумма
сумма ![]() положительна. Тогда транспонирование матрицы
положительна. Тогда транспонирование матрицы ![]() , где
, где
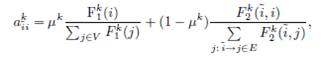 (10)
(10)
является стохастическим. Поэтому существует [20] стационарное распределение ![]() , которое является единственным решением Уравнения 8, удовлетворяющим условию
, которое является единственным решением Уравнения 8, удовлетворяющим условию ![]() .
.
4. ОБУЧЕНИЕ
В этом разделе представлено теоретическое обоснование для параметрической оптимизации метода SNP, который мы ввели в 3.2. Во-первых, мы опишем линейные уравнения, которые определяют производные стационарного распределения π. Во-вторых, мы представим алгоритм решения этих уравнений.
4.1 Вычисление производных
Рассмотрим граф G и задачи 1…, R, которые определены в Разделе 3.1. Напомним, что компоненты стационарного распределения марковского процесса π, введенного в Разделе 3.2, определяют решение задачи q (в некоторых случаях свойства узлов и ребер независимы от нее, а в некоторых – зависимы, в этих случаях ![]() , где π — стационарное распределение, а bq — исходная весовая функция, зависимая от задачи). Подчеркнем, что
, где π — стационарное распределение, а bq — исходная весовая функция, зависимая от задачи). Подчеркнем, что ![]() зависит от вектора параметров
зависит от вектора параметров ![]() , где согласно Разделу 3.2 χ – вектор, состоящий из компонентов ω, компонентов φ, и α, μ1, μ2. Мы минимизируем целевую функцию F, определенную в Разделе 3.1 градиентным методом оптимизации. Согласно Уравнению 4, функция F является композицией H и πq, так что
, где согласно Разделу 3.2 χ – вектор, состоящий из компонентов ω, компонентов φ, и α, μ1, μ2. Мы минимизируем целевую функцию F, определенную в Разделе 3.1 градиентным методом оптимизации. Согласно Уравнению 4, функция F является композицией H и πq, так что
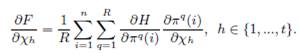
Очевидно, что производные H относительно всех ее аргументов легко вычисляются, т.к. для среднеквадратической ошибки измерений ![]() . Таким образом, главную трудность представляет вычисление производных
. Таким образом, главную трудность представляет вычисление производных ![]() . В SSP производные
. В SSP производные ![]() и
и ![]() существуют и могут быть определены на основе следующих систем уравнений:
существуют и могут быть определены на основе следующих систем уравнений:
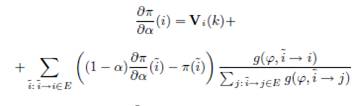
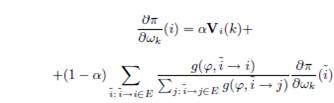
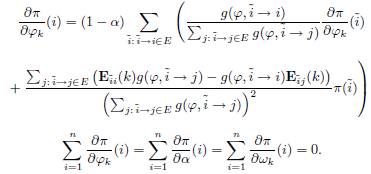
Чтобы найти производные для нашей методологии, введенной в Разделе 3.2, перепишем Уравнение 3 в матричной форме:
![]() (11)
(11)
где ![]() и
и
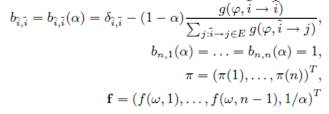 (12)
(12)
![]()
Подчеркнем, что мы убрали одно уравнение π(i) из (3), которое соответствует случаю i = n. Фактически, (3) эквивалентно системе ![]() , тогда сумма первых уравнений (3) i = 1, 2..., n равна последнему уравнению
, тогда сумма первых уравнений (3) i = 1, 2..., n равна последнему уравнению ![]() из той же системы. Теперь введем системы линейных уравнений для вычисления производных
из той же системы. Теперь введем системы линейных уравнений для вычисления производных ![]() . Аналогичные системы для других производных можно построить таким же способом.
. Аналогичные системы для других производных можно построить таким же способом.
ЛЕММА 1. Функции π(i) дифференцируемы относительно ![]() . Кроме того, производные
. Кроме того, производные ![]() являются решениями следующих систем линейных уравнений:
являются решениями следующих систем линейных уравнений:
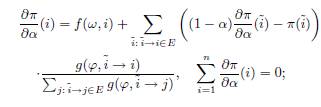 (13)
(13)
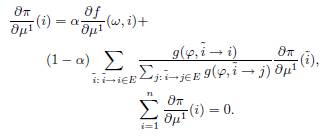 (14)
(14)
Наконец, производная ![]() может быть найдена на основе следующей системы:
может быть найдена на основе следующей системы:
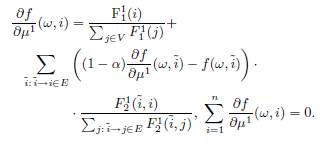 (15)
(15)
Доказательство. Т.к. функции ![]() — полиномы первой степени, решение
— полиномы первой степени, решение ![]() (11) состоит из вещественных функций α. Таким образом, π(i) дифференцируемы относительно α в любой точке (0, 1). Рассмотрим левую и правую части Уравнения 3 как две функции от α, заданные в неявном виде. Если π — решение системы, то значения этих двух функций равны для любого α из (0, 1). Поэтому производные этих функций относительно α также равны. Т.к. функции
(11) состоит из вещественных функций α. Таким образом, π(i) дифференцируемы относительно α в любой точке (0, 1). Рассмотрим левую и правую части Уравнения 3 как две функции от α, заданные в неявном виде. Если π — решение системы, то значения этих двух функций равны для любого α из (0, 1). Поэтому производные этих функций относительно α также равны. Т.к. функции ![]() и
и ![]() независимы от α, мы получаем Уравнение 13.
независимы от α, мы получаем Уравнение 13.
Аналогично можно доказать, что ![]() вещественная функция от μ1. Таким образом, она дифференцируема относительно μ1 в каждой точке (0, 1), и мы получаем Уравнение 15. Кроме того, вектор π состоит из вещественных функций
вещественная функция от μ1. Таким образом, она дифференцируема относительно μ1 в каждой точке (0, 1), и мы получаем Уравнение 15. Кроме того, вектор π состоит из вещественных функций ![]() , которые при этом являются и вещественными функциями от μ1. Таким образом π(i) также дифференцируемы относительно μ1 в каждой точке (0, 1).
, которые при этом являются и вещественными функциями от μ1. Таким образом π(i) также дифференцируемы относительно μ1 в каждой точке (0, 1).
Рассмотрим левую и правую части Уравнения 3 как две функции от μ1. Согласно (3) производные этих функций относительно μ1 равны. Т.к. функция ![]() независима от μ1, мы получаем Уравнение 14. Таким образом, существование производных
независима от μ1, мы получаем Уравнение 14. Таким образом, существование производных ![]() доказано.
доказано.
Лемма 1 описывает уравнения, которые определяют производные π относительно параметров α, μ1. Отметим, что все другие производные ![]() могут быть найдены аналогичным способом, и мы не приводим соответствующие уравнения и доказательства, чтобы не загромождать статью.
могут быть найдены аналогичным способом, и мы не приводим соответствующие уравнения и доказательства, чтобы не загромождать статью.
В Разделе 4.2 представлен алгоритм численного решения систем (Лемма 1), выходом которого являются производные ![]() . Насколько нам известно, мы первые, кто получил градиенты стационарных распределений вложенных марковских процессов относительно их параметров.
. Насколько нам известно, мы первые, кто получил градиенты стационарных распределений вложенных марковских процессов относительно их параметров.
4.2 Обучающий алгоритм
В этом разделе описывается наш алгоритм вычисления градиентов стационарных распределений вложенных марковских процессов относительно их параметров. Полученные градиенты используются для нахождения оптимальных значений этих параметров. Данный алгоритм основан на системах линейных уравнений предыдущего раздела (см. Лемму 1). Для демонстрации метода рассмотрим только случай производных ![]() , опустив аналогичные случаи для всех других производных, чтобы не загромождать статью.
, опустив аналогичные случаи для всех других производных, чтобы не загромождать статью.
Запишем Уравнение 3 в следующей форме: ![]() , где
, где ![]()
![]() (16)
(16)
Согласно эргодической теореме [16], для любого начального распределения π0 для множества вершин V, стационарное распределение π, определенное Уравнением 3, равняется ![]() . Выразим
. Выразим ![]() через πj. Очевидно
через πj. Очевидно
![]() (17)
(17)
Пусть ![]() . Из Леммы 1 следует, что существует производная
. Из Леммы 1 следует, что существует производная ![]() . Найдем производные обеих частей Уравнения 17 относительно
. Найдем производные обеих частей Уравнения 17 относительно ![]() :
:
![]() (18),
(18),
где
![]()
Рассмотрим также Уравнение 8 и перепишем его в следующей форме: ![]() , где
, где ![]() , и для каждой
, и для каждой ![]() определяются Уравнением 10.
определяются Уравнением 10.
Согласно эргодической теореме, для любого ![]() и любого распределения
и любого распределения ![]() выполняется равенство
выполняется равенство ![]() . Выразим
. Выразим ![]() через
через ![]() . Получим
. Получим
![]() (19)
(19)
Найдем производные обеих частей Уравнения 19 для случая k = 1 относительно μ1:
![]() (20),
(20),
где
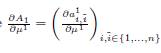
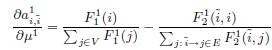 (21)
(21)
ТЕОРЕМА 1. Для любого ![]() справедливо
справедливо
![]() .
.
Доказательство теоремы приведено в Приложении A. На ее основе при помощи (18) можно найти приблизительные значения ![]() и
и ![]() . Фактически мы можем использовать следующую последовательность действий. Во-первых, мы итеративно вычисляем значения
. Фактически мы можем использовать следующую последовательность действий. Во-первых, мы итеративно вычисляем значения ![]() при помощи Уравнений 19–21. Затем мы находим элементы матриц
при помощи Уравнений 19–21. Затем мы находим элементы матриц ![]() , используя
, используя
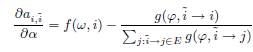
![]() (22).
(22).
Наконец, после того, как получены значения ![]() , рекурсивно используем Уравнения 17–18, чтобы вычислить
, рекурсивно используем Уравнения 17–18, чтобы вычислить ![]() . Согласно Теореме 1 полученные значения являются приближением
. Согласно Теореме 1 полученные значения являются приближением ![]() . Данный алгоритм представлен в Таблице 1.
. Данный алгоритм представлен в Таблице 1.
Таблица 1: Итеративный алгоритм вычисления производных μ1 стационарного распределения Supervised Nested PageRank.
| Вход: Выход: Алгоритм: 1. Вычислить 2. Вычислить 3. Установить 4. Обновить 5. Если 6. Установить 7. Вычислить 8. Установить 9. Обновить 10. Если |
5. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ЭКСПЕРИМЕНТОВ
В этом разделе разбираются на практике два варианта задачи ранжирования графа, на основе которых будет проводиться экспериментальное оценивание. Определяются целевые функции, все параметры марковских процессов и вводятся настройки обучения.
5.1 Целевая функция
Данные, которые используются для настройки параметров ![]() (см. Раздел 4) представляют собой коллекцию запросов пользователей Yandex. Для каждого запроса q существуют наборы страниц, оцененные вручную и сгруппированные по релевантностям. Обозначим эти группы как
(см. Раздел 4) представляют собой коллекцию запросов пользователей Yandex. Для каждого запроса q существуют наборы страниц, оцененные вручную и сгруппированные по релевантностям. Обозначим эти группы как ![]() в порядке убывания их релевантностей. Пусть для любых двух страниц
в порядке убывания их релевантностей. Пусть для любых двух страниц ![]()
![]() будет штрафной функцией, которая используется в случае, если позиция страницы p2 согласно нашей ранжирующей функции dq будет выше позиции страницы p1, и при этом i<j. Будем рассматривать штраф h с ограничением bij>0, где
будет штрафной функцией, которая используется в случае, если позиция страницы p2 согласно нашей ранжирующей функции dq будет выше позиции страницы p1, и при этом i<j. Будем рассматривать штраф h с ограничением bij>0, где ![]() , то есть
, то есть ![]() . Согласно Разделу 3.1, цель оптимизации — минимизация функции
. Согласно Разделу 3.1, цель оптимизации — минимизация функции
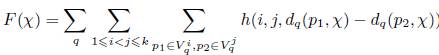 (23)
(23)
где
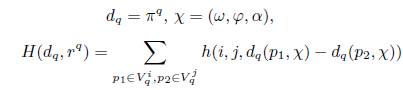
Мы предлагаем сделать это при помощи градиентного метода оптимизации, описанного в [25]. Используем алгоритм, описанный в Разделе 4.2, для вычисления производных. Наш метод оптимизации достаточно эффективен: его сложность равна числу итераций градиентного спуска, умноженному на сложность алгоритма PageRank.
В следующих двух разделах будут описаны свойства, которые влияют на веса узлов во вложенных марковских процессах (скалярные величины ![]() ). Все эти характеристики и конечные веса не зависят от запросов. Тогда чтобы сравнить работу алгоритмов для исследования задачи ранжирования, зависимого от запроса, как в [7], будем рассматривать линейную комбинацию независимых весов π со значениями BM25 страниц bq, которые являются запросозависимыми (см. Уравнение 5). Оценивать полученные результаты будем на основе метрики Normalized Discounted Cumulative Gain (NDCG). Параметр линейной комбинации λ выбирается на первой итерации градиентного спуска из условия максимизации NDCG на обучающей выборке. На последующих итерациях новые значения параметра определяются по формуле:
). Все эти характеристики и конечные веса не зависят от запросов. Тогда чтобы сравнить работу алгоритмов для исследования задачи ранжирования, зависимого от запроса, как в [7], будем рассматривать линейную комбинацию независимых весов π со значениями BM25 страниц bq, которые являются запросозависимыми (см. Уравнение 5). Оценивать полученные результаты будем на основе метрики Normalized Discounted Cumulative Gain (NDCG). Параметр линейной комбинации λ выбирается на первой итерации градиентного спуска из условия максимизации NDCG на обучающей выборке. На последующих итерациях новые значения параметра определяются по формуле: ![]() , где τ — постоянная величина шага градиентного спуска,
, где τ — постоянная величина шага градиентного спуска, ![]() — номер итерации.
— номер итерации.
Отметим, что в [7] авторы используют другую целевую функцию, ![]() , где π(i) равняется
, где π(i) равняется
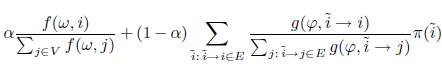
Поскольку эта функция запросонезависимая, и решение задачи оптимизации не учитывает оценки релевантностей документов, авторы вводят ограничения на использованиЕ своей технологии. Подчеркнем, что для любого положительного ε мы можем найти вектор π, такой, что ![]() , используя итеративный алгоритм из Таблицы 1. Поэтому любой локальный минимум целевой функции является соответствующим минимумом функции
, используя итеративный алгоритм из Таблицы 1. Поэтому любой локальный минимум целевой функции является соответствующим минимумом функции ![]() с ограничением вида
с ограничением вида ![]() , где С — некоторое положительное число. Таким образом, получено решение задачи оптимизации для алгоритмов SSP и SNP. Кроме того, вектор высокой размерности является параметром функции R, в то время как целевая функция F не зависит от него. Следовательно, предложенный метод оптимизации имеет значительно меньшую размерность, а потому является на порядки более быстрым с вычислительной точки зрения.
, где С — некоторое положительное число. Таким образом, получено решение задачи оптимизации для алгоритмов SSP и SNP. Кроме того, вектор высокой размерности является параметром функции R, в то время как целевая функция F не зависит от него. Следовательно, предложенный метод оптимизации имеет значительно меньшую размерность, а потому является на порядки более быстрым с вычислительной точки зрения.
5.2 Параметры графов
В наших экспериментах будем использовать дискретные марковские процессы на основе ссылочного графа. Все эксперименты проводились на базе графа, состоящего из страниц и ссылок, составляющих индекс Яндекса на июнь 2013 года. Используемая коллекция документов собрана в доменном пространстве одной из крупнейших европейских стран. Множество данных содержит 2.52 миллиарда страниц и 21.12 миллиарда ссылок. Так как его размерность очень велика, мы использовали модель Pregel [24] для параллельных вычислений (граф был разбит случайным образом на 700 частей). Чтобы определить веса узлов и ребер, будем рассматривать два множества свойств страниц: используемые SSP в оригинальной статье [7] и временные свойства, представленные ниже.
Как было предположено в [7], для каждого ребра в графе используем десять свойств, включая тип ссылки (т.е., внутренняя или внешняя), количество входящих и исходящих ссылок для донора и акцептора (всего четыре свойства), уровень вложенности URL и длина URL для донора и акцептора (всего четыре свойства), и вес (количество ссылок) ребра. Для каждого узла мы используем 5 свойств, включая количество входящих и исходящих ссылок страницы, количество «двухшаговых» соседей страницы, уровень вложенности и длину URL страницы.
Используем данные из [26] (в которой обобщена модель из [5]) для временных свойств (см. Раздел 2). Пусть T — временной период, который начинается с 1 января 2013. Тогда ![]() , если страница p создана в период T, иначе
, если страница p создана в период T, иначе ![]() .
. ![]() и
и ![]() количества ссылок
количества ссылок ![]() и
и ![]() соответственно, созданных в период T так, что по крайней мере одна из страниц p, ˜p появилась после 1 января 2013.
соответственно, созданных в период T так, что по крайней мере одна из страниц p, ˜p появилась после 1 января 2013. ![]() и
и ![]() являются количеством ссылок
являются количеством ссылок ![]() и
и ![]() соответственно, созданных в период T так, что страницы p, ˜p появились ранее 1 января 2013. Рассмотрим следующие временные веса узлов и ребер.
соответственно, созданных в период T так, что страницы p, ˜p появились ранее 1 января 2013. Рассмотрим следующие временные веса узлов и ребер.
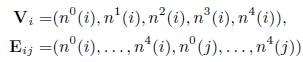 (24)
(24)
Здесь h = 10, l = 5, где l — число свойств узлов, h — число свойств ребер (см. Раздел 3.1).
Для всех методов мы нашли оптимальные значения параметров, минимизирующие целевую функцию F (23) на основе градиентого метода оптимизации (см. Раздел 4.2 и Раздел 5.1). Для ранжирования было сформировано множество запросов, которые задают пользователи одной из европейских стран. Для каждого запроса было проведено оценивание множества страниц профессиональными асессорами, нанятыми Яндексом. Эксперт оценивает пару <запрос, URL> на основе новизны и релевантности страницы относительно запроса. Оценки релевантности выбираются по распространенной шкале: perfect, excellent, good, fair, bad. Данные, которые мы использовали, содержат 126.4 тысячи пар запрос-URL и 16.7 тысяч запросов. Мы выбрали 90% запросов в качестве обучающей выборки для оптимизации параметров. Далее мы сравнили методы на основе усредненной метрики NDCG, вычисленной по оставшимся 10% запросов (тестовая выборка). Подчеркнем, что NDCG вычислялась на обрезанном множестве документов, которое было получено из исходного множества, путем удаления всех неоцененных страниц. Данный подход является наилучшим в условиях неполных оценок [19]. Формат нашего экспериментального исследования более адекватен реальности и поисковой индустрии нежели применяемый авторами SSP, которые оценивали документы тестовой выборки, используя бинарную шкалу релевантностей, и обучали SSP на зашумленных неявных оценках, построенных непосредственно на базе подсчетов кликов на документ.
6. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
Оценим алгоритм SNP и алгоритм SSP, используя свойства, описанные в предыдущем разделе. В качестве базы для обоих алгоритмов будем использовать PageRank (как в статье [7]). В Таблице 2 представлены результаты оценивания ранжирования алгоритмов на основе метрик NDCG@3 и NDCG@5.
Таблица 2. Сравнение SSP и SNP
|
Тип свойств |
Итерация |
Метод |
NDCG@3 |
@5 |
|
SSP + [7] |
Первая |
SSP |
0.76326 |
0.79902 |
|
SNP |
0.76522 |
0.79964 |
||
|
SSP + [7] |
Последняя |
SSP |
0.76534 |
0.80007 |
|
SNP |
0.76909 |
0.80368 |
||
|
Временные |
Первая |
SSP |
0.76336 |
0.80208 |
|
|
SNP |
0.76432 |
0.80031 |
|
|
Временные |
Последняя |
SSP |
0.7688 |
0.80426 |
|
SNP |
0.77543 |
0.80753 |
Согласно NDCG@3 (@5) преимущество метода SNP по сравнению с SSP составляет 0.8% (0.4%) и 0.5% (0.5%) для временных свойств и свойств SSP соответственно. Это преимущество нельзя рассматривать как незначительное с точки зрения исследуемой задачи ранжирования. Действительно, по NDCG@3 (@5) преимущество метода SSP по сравнению с PageRank составляет 0.4% (0.8%) и для временных свойств и для свойств SSP на нашей коллекции веб-страниц (см. рисунок 1, рисунок 2). Т.е. превосходство SSP над PageRank имеет тот же самый порядок (1% для NDCG@3) в [7]. Кроме того, отранжированные в [7] документы могут быть переоценены, потому что каждый из них оценивался как “релевантный” или “нерелевантный”, в то время как в нашем исследовании использовалась 5-ти ступенчатая шкала релевантности. Также алгоритм BrowseRank [13], основанный на графе случайных блужданий пользователя, имеет преимущество в 1.6% (NDCG@3) по сравнению с PageRank (см. [13]).
Полученные результаты парных тестов для оценки различия между SNP и SSP (во всех случаях) на экспериментальных данных говорят о том, что SNP значительно выигрывает у SSP (см. строки в Таблице 2, соответствующие последним итерациям).
Первоначально PageRank вычислялся с коэффициентом затухания α=0.15. Для демонстрации важности настройки параметров проведем следующие эксперименты. Во-первых, сравним результаты алгоритмов, использующих временные свойства, соответствующих оптимальным значениям параметров, с алгоритмами с теми же настройками за исключением α, который мы приравняем 0.15 (см. Таблицу 2 и Таблицу 3). Как видно, обучение дает лучшие результаты с точки зрения NDCG@3, @5 (обученные алгоритмы имеют статистически значимое превосходство по сравнению с вышеупомянутыми модификациями). Во-вторых, настройка коэффициента затухания α в классическом алгоритме PageRank (PR), дает лучший результат по сравнению с исходным вариантом (PR ++) (см. Таблицу 3, рисунок 1, рисунок 2). Полученный на основе обучения параметр равен 0.9514.
Таблица 3. Результаты алгоритмов SSP и SNP с α =0.15 и PageRank с α =0.15, α =0.9514
| Algorithm | NDCG@3 | NDCG@5 |
| Temporal SSP, α = 0.15 |
0.76542 | 0.80215 |
| Temporal SNP, α = 0.15 |
0.76938 | 0.80491 |
| PageRank, α = 0.15 |
0.76256 | 0.79749 |
| PageRank, α = 0.9514 |
0.76525 | 0.7998 |
Таблица 4. Результаты алгоритма дляSNP c μ1 = μ2 = 0
| Algorithm, μ1 = μ2 = 0 | NDCG@3 | NDCG@5 |
| Temporal SNP | 0.76535 | 0.79929 |
| SNP, features from [7] | 0.75755 | 0.79465 |
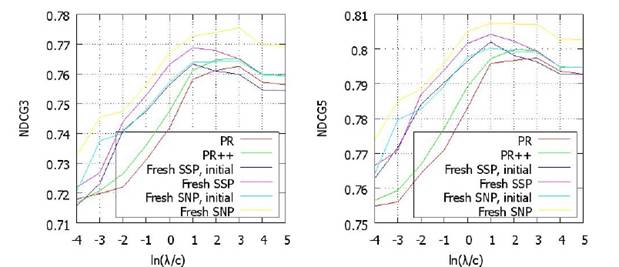
Рисунок 1. Результаты для различных значений λ (используются временные свойства). Алгоритмы: SNP, SNP с начальными параметрами, SSP, SSP с начальными параметрами, PageRank (PR), PageRank c α=0.9514 (PR++)
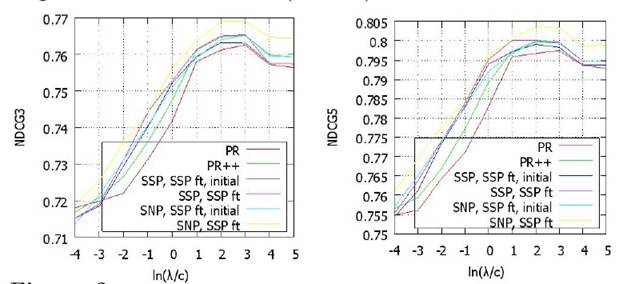
Рисунок 2. Результаты для различных значений λ (используются свойства SSP). Алгоритмы: SNP, SNP с начальными параметрами, SSP, SSP с начальными параметрами, PageRank (PR), PageRank c α=0.9514 (PR++)
Отметим, что SNP сводится к SSP, если установить μ1 = μ2 = 1. Рассмотрим другой граничный случай μ1 = μ2 = 0, обучив остальные параметры. NDCG@3,5 этих “экстремальных алгоритмов” показаны в Таблице 4. Оценки качества ранжирования всех этих алгоритмов представлены на рисунках 1-2. Из графиков видно, что максимальные значения NDCG@3, @5 по всей области значений λ больше для SNP в обоих случаях (временные свойства и свойства SSP).
Далее в этом разделе мы покажем, как в алгоритме SNP решается проблема разреженности данных. Мы считаем, что только репрезентативная выборка исходного графа позволит ускорить вычисления в этой части экспериментов. Пусть для любого запроса q H (q) — множество хостов, имеющих по крайней мере одну страницу p релевантную q. L (q) — количество внутренних ссылок на хостах из H(q). Выберем множество X, которое состоит из 12% запросов q с самыми маленькими значениями мощности |L(q)|. Построим начальный граф на основе всех страниц множества ![]() и всех ссылок между ними.
и всех ссылок между ними.
Получим 0.11 миллиардов страниц (4.4% количества вершин в полном графе) и 2.1 миллиарда ссылок (9.9% количества ребер в полном графе). Обучающая выборка состоит из 8327 пар <запрос, URL> и 1990 запросов. Тестовая выборка состоит из 726 пар <запрос, URL> и 187 запросов. Сымитируем разреженность данных, выбирая для каждого временного свойства r% страниц, r ={10, 25, 50, 90}, и удаляя значения данного свойства у этих страниц. На полученном графе вычислим SNP и SSP, показав, что разреженность данных затрагивает SSP существенно сильнее, чем SNP (см. рисунок 3).
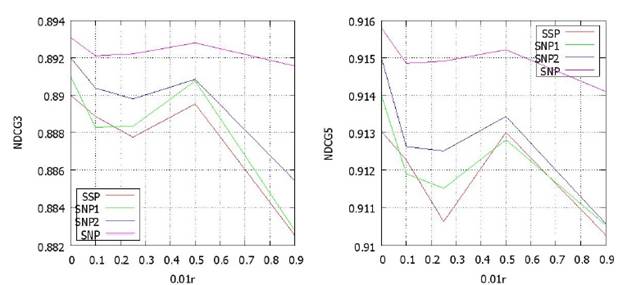
Рисунок 3: Разреженность данных.
Сравним SNP с его модификациями, которые не дожидаются выполнения условия остановки сглаживания весов вершин и ребер. Другими словами, рассмотрим измененный алгоритм из Таблицы 1, в котором производится ![]() итераций шага 4, где
итераций шага 4, где ![]() — небольшое число. После
— небольшое число. После ![]() итераций рассчитываются значения
итераций рассчитываются значения ![]() по уравнениям шага 5. Отметим, что если приравнять
по уравнениям шага 5. Отметим, что если приравнять ![]() нулю и вычислить G1 и G2 на шаге 3, то мы получим обычный SSP. Попробуем показать, как значение
нулю и вычислить G1 и G2 на шаге 3, то мы получим обычный SSP. Попробуем показать, как значение ![]() влияет на результаты SNP на разреженном множестве данных. Предположительно, стабильность результата тем выше, чем больше итераций производится. Сравним четыре алгоритма, SSP (
влияет на результаты SNP на разреженном множестве данных. Предположительно, стабильность результата тем выше, чем больше итераций производится. Сравним четыре алгоритма, SSP (![]() = 0), SNP1 (
= 0), SNP1 (![]() = 1), SNP2 (
= 1), SNP2 (![]() = 2) и SNP. На рисунке 3 представлены результаты ранжирования на их основе. Обучающий алгоритм для параметров SNP1 и SNP2 такой же, что и SNP. Целевая функция, параметры настройки для метода градиентного спуска у них также одинаковые. Производные вычислены на базе алгоритма из Таблицы 1, но со следующими отличиями. Шаг 4 повторяется 1 раз для SNP1 и дважды для SNP2. Как видно, результаты SNP более стабильны, по сравнению с SSP, SNP1 и SNP2, что говорит о важности повторения итераций (шага 4) до выполнения условия остановки.
= 2) и SNP. На рисунке 3 представлены результаты ранжирования на их основе. Обучающий алгоритм для параметров SNP1 и SNP2 такой же, что и SNP. Целевая функция, параметры настройки для метода градиентного спуска у них также одинаковые. Производные вычислены на базе алгоритма из Таблицы 1, но со следующими отличиями. Шаг 4 повторяется 1 раз для SNP1 и дважды для SNP2. Как видно, результаты SNP более стабильны, по сравнению с SSP, SNP1 и SNP2, что говорит о важности повторения итераций (шага 4) до выполнения условия остановки.
ЗАКЛЮЧЕНИЕ
В этой статье была представлена новая общая модель ранжирования, которая основана на графе и определяется случайным блужданием с учетом весов узлов и ребер, которые в свою очередь определяются вложенными случайными блужданиями с учетом их свойств. Параметры модели обучаются на основе эффективного алгоритма оптимизации. Полученные результаты экспериментальных исследований показали, что алгоритм превосходит современную технологию SSP, основанную на значительно более простом методе взвешивания узлов и ребер, использующем их свойства.
Продолжение изучения свойств нашего алгоритма и аспектов его применения представляет определенный интерес. Планируется провести исследования по следующим направлениям. Во-первых, провести эксперименты с другими классами данных (например, с использованием непрерывных марковских процессов), с другими типами графов (например, граф пользовательских просмотров), с другим набором свойств, которые определяют веса узлов и ребер. Во-вторых, провести исследования в области повышения скорости сходимости метода градиентного спуска, используемого для целевой функции. В-третьих, более подробно исследовать вопрос влияния числа итераций в процессе вычисления весов на ранжирование и его результаты (с точки зрения целевой функции или других метрик).
8. ССЫЛКИ НА ЛИТЕРАТУРУ
[1] L. Backstrom, J. Leskovec, Supervised random walks: predicting and recommending links in social networks, WSDM’11.
[2] K. Berberich, M. Vazirgiannis, G. Weikum, Time-aware authority ranking, Int. Math., 2(3), pp. 301–332, 2005.
[3] S. Chakrabarti, A. Agarwal, Learning parameters in entity relationship graphs from ranking preferences, PKDD’06.
[4] H. Chang, D. Cohn, A. K. McCallum, Learning to create customized authority lists, ICML’00.
[5] Na Dai and Brian D. Davison, Freshness Matters: In Flowers, Food, and Web Authority, SIGIR’10.
[6] Nadav Eiron, Kevin S. McCurley, John A. Tomlin, Ranking the web frontier, WWW’04.
[7] B. Gao. Tie-Yan Liu, Wei Wei Huazhong, T. Wang, H. Li, Semi-supervised ranking on very large graphs with rich metadata, KDD’11.
[8] Taher H. Haveliwala, Efficient computation of PageRank, Stanford University Technical Report, 1999.
[9] Taher H. Haveliwala, Topic-Sensitive PageRank, WWW’2002.
[10] N. Kanhabua, K. Nørv°ag, Improving Temporal Language Models for Determining Time of Non-timestamped Documents, ECDL’08.
[11] J. M. Kleinberg, Authoritative sources in a hyperlinked environment, SODA’98.
[12] Ni Lao, William W. Cohen, Relational retrieval using a combination of path-constrained random walks, Journal Machine Learning archive, 81(1), pp. 53–67, 2010.
[13] Y. Liu, B. Gao, T.-Y. Liu, Y. Zhang, Z. Ma, S. He, H. Li, BrowseRank: Letting Web Users Vote for Page Importance, SIGIR’08.
[14] Y. Liu, M. Zhang, S. Ma, L. Ru, User Browsing Graph: Structure, Evolution and Application, WSDM’09.
[15] E. Minkov, William W. Cohen, Learning to rank typed graph walks: local and global approaches, KDD’07.
[16] J. R. Norris, Markov Chains, Cambridge University, 1998.
[17] L. Page, S. Brin, R. Motwani, and T. Winograd, The PageRank citation ranking: Bringing order to the web. https://dbpubs.stanford.edu/pub/1999-66, 1999.
[18] M. Richardson, P. Domingos, The intelligent surfer: Probabilistic combination of link and content information in PageRank, Neural Information Processing Systems, 14, pp. 1441–1448, 2002.
[19] T. Sakai, Alternatives to Bpref, SIGIR ’07.
[20] W. J. Stewart, Introduction to the Numerical Solution of Markov Chains, Princeton University, N.J., 1994.
[21] A. C. Tsoi, G. Morini, F. Scarselli, M. Hagenbuchner, M. Maggini, Adaptive ranking of Web pages, WWW’03.
[22] D. Zhou, J. Huang, B. Scholkopf, Learning from labeled and unlabeled data on a directed graph, ICML’05.
[23] J. Gao, W. Yuan, X. Li, K. Deng, J.-Y. Nie, Smoothing Clickthrough Data for Web Search Ranking, SIGIR’09.
[24] G. Malewicz, M. H. Austern, A. J. C. Bik, J. C. Dehnert, I. Horn, N. Leiser, G. Czajkowski, Pregel: A System for Large-Scale Graph Processing, SIGMOD’10.
[25] J. A. Snyman, Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms, Springer, 2005.
[26] M. Zhukovskii, D. Vinogradov, G. Gusev, P. Serdyukov, A. Raigorodkii, Recency-sensitive model of web page authority, CIKM’12.
[27] M. Zhukovskii, A. Khropov, G. Gusev, P. Serdyukov, Fresh BrowseRank, SIGIR’13.
ПРИЛОЖЕНИЕ A. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1
Из Леммы 1 известно, что функции ![]() дифференцируемы относительно α и μ1
дифференцируемы относительно α и μ1 ![]() . Пусть
. Пусть ![]() — произвольное число. Т.к.
— произвольное число. Т.к. ![]() , то существует i, такое, что
, то существует i, такое, что ![]() . Тогда существует
. Тогда существует ![]() и столбец i0 матрицы АТ, такой, что
и столбец i0 матрицы АТ, такой, что ![]()
![]()
![]() . Поэтому сходимость
. Поэтому сходимость ![]() равномерна для
равномерна для ![]() (см. [16]) и, кроме того, существует число
(см. [16]) и, кроме того, существует число ![]() , такое, что для довольно большого j выполняется неравенство
, такое, что для довольно большого j выполняется неравенство ![]() .
.
Положим ![]() . Из Уравнения 18 и Уравнения 13, которое можно переписать в виде
. Из Уравнения 18 и Уравнения 13, которое можно переписать в виде ![]() , получим
, получим
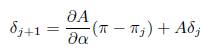 .
.
Пусть γ — любое положительное число, а* — максимальный по модулю элемент ![]() . Тогда существует
. Тогда существует ![]() , такое, что модуль каждого элемента
, такое, что модуль каждого элемента ![]() меньше
меньше ![]() для всех
для всех ![]() . Т.к.
. Т.к. ![]() и
и ![]() стохастические, то модуль каждого элемента
стохастические, то модуль каждого элемента ![]() меньше
меньше ![]() .
.
Выберем j, такое, что ![]() . Отметим, что для любого n-мерного вектора ε, такого, что сумма его элементов равняется 0, мы имеем
. Отметим, что для любого n-мерного вектора ε, такого, что сумма его элементов равняется 0, мы имеем ![]() .
.
Действительно, если ε* — максимальный модуль элементов ε, тогда разностью n-мерного вектора ![]() и является некоторое распределение
и является некоторое распределение ![]() . Поэтому
. Поэтому ![]() . Кроме того,
. Кроме того, ![]() . Так что
. Так что ![]()
Поэтому существует k0, такое, что для любого ![]() любой элемент
любой элемент ![]() меньше, чем γ/2. Наконец, для любого
меньше, чем γ/2. Наконец, для любого ![]() любой элемент δj меньше, чем γ. Так мы получаем
любой элемент δj меньше, чем γ. Так мы получаем ![]() . Таким образом сходимость
. Таким образом сходимость ![]() доказана.
доказана.
Аналогично существует ![]() , такое, что
, такое, что ![]() и, следовательно, для некоторых δ>0 и любой
и, следовательно, для некоторых δ>0 и любой ![]() выполняется неравенство
выполняется неравенство ![]() . Таким образом, для фиксированного
. Таким образом, для фиксированного ![]() выполняется следующее свойство i0-го столбца АТ:
выполняется следующее свойство i0-го столбца АТ: ![]() .
.
Сходимость ![]() для любого
для любого ![]() следует из равномерной сходимости
следует из равномерной сходимости ![]() со скоростью pj для
со скоростью pj для ![]() .
.
Сходимость ![]() доказывается таким же образом как сходимость
доказывается таким же образом как сходимость ![]() .
.
Разъяснения к статье Ильи Зябрева и Олега Пожаркова:
Статья, посвященная новой модели, именуемой Supervised Nested PageRank (SNP), дословный перевод названия которой означает что-то вроде Управляемый Вложенный PR, исключительно с научной точки зрения весьма и весьма хороша. Данная разработка «ученых Яндекса» представляет собой мощную теоретическую технологию, предназначенную для решения большого количества разнообразных задач, в том числе и в области информационного поиска. А вот ее практическая полезность пока вызывает сомнения, по крайней мере, представленные в статье результаты не впечатляют. Но обо всем по порядку.
Чтобы перейти к рассмотрению того, чем на самом деле является SNP и чем он отличается от старого доброго PR, уделим немного внимания теории графов и ее использованию в задачах ранжирования.
Граф, по сути, – это множество вершин (узлов) и ребер (дуг), которые их соединяют. В виде графа удобно представлять многие реальные или виртуальные объекты. Например, ссылочный граф (который используется для множества поисковых задач, в том числе и для вычисления PR) представляет собой совокупность веб-страниц (узлов) и ссылок, которые их связывают (ребер). Причем эти ребра направленные, т.е. одна страница ссылается на другую, и, соответственно, граф тоже направленный. Другими примерами графов могут служить граф переходов пользователя (используется для BrowseRank, страницы – вершины, а переходы между ними по ссылкам – ребра), граф связей между пользователями в социальных сетях (вершины – пользователи, если два пользователя – друзья, то между ними есть ребро) и т.д. Т.е. использование графа для различных задач, связанных с информационным поиском, довольно распространенное явление. Одним из первых его применений в этой области был именно PageRank, с которого, по сути, начал формироваться класс задач ранжирования на основе графа. Как это работает? Об этом ниже. Если вы хорошо представляете себе механизм определения PageRank на основе графа, эту часть можно пропустить.
Ключевыми понятиями для решения задачи ранжирования являются понятия веса вершин (страниц в случае PageRank) и случайного блуждания, благодаря которому происходит «перенос» весов с вершины на вершину через связывающие их ребра (ссылки). Чтобы объяснить, что такое случайное блуждание в данном случае, представим некоторого пользователя, который не умеет читать и перемещается по сайтам случайным образом, т.е. его не интересует ни содержание страниц, ни текст ссылок, по которым он скачет. В начальный момент времени он может выбрать случайным образом любую вершину графа. Т.е. вероятность того, что он выберет конкретную страницу, равна 1/N (N – число страниц). Это начальный вес каждой страницы (начальная вероятность). На каждом последующем шаге пользователь может перейти либо по любой ссылке (выбранной случайным образом, естественно) со страницы, на которой он находится в данный момент, либо остаться на этой странице. Вероятность, с которой пользователь остается, называется коэффициентом затухания α, и в классическом алгоритме PR она равна 0,15. Соответственно, вероятность, с которой он пойдет дальше, равна 1-0,15=0,85. При этом вероятность того, что он выберет одну из страниц, на которую ведут ссылки с данной равна m/M (m – число (кратность) ссылок с данной страницы на выбранную, M – общее число исходящих ссылок с данной страницы).
Отметим важный момент: если со страницы (узел) 1 есть хотя бы одна ссылка на страницу 2, то между соответствующими вершинами графа есть ребро, кратность которого равна количеству ссылок с 1 на 2. Таким образом, вероятность m/M (вероятность перехода из одного узла в другой) является, по сути, весом ребра (соединяющего эти узлы). А теперь представим, что пользователь бесконечно совершает свои «шаги», т.е. выбирает, остаться ли на странице или пойти по ссылке, и нам нужно определить, какую страницу он просматривает в данный момент, учитывая, что начал он свои блуждания давным-давно. Логичнее всего искать его на странице с наибольшим числом входящих ссылок (с как можно большего числа других страниц) и в идеале ни одной исходящей, т.е. вероятность того, что пользователь находится в данный момент на ней, будет максимальной. Для других страниц данная вероятность будет аналогично определяться количеством входящих и исходящих ссылок, а также весами их доноров. Эти вероятности называются стационарными (т.к. при достаточно большом числе «шагов» они не изменяются) и являются, по сути, конечными весами страниц.
Случайное блуждание можно представить следующим образом: на каждую страницу выделяется некоторый начальный вес, а пользователь бегает между ними по ссылкам, перетаскивая эти веса. Страницы, на которые он чаще заходит во время своих странствий, в итоге получают больше веса, на которые реже – меньше. Конечный вес и есть исходная оценка для PR, на основе которой производится ранжирование. Такая «пошаговая» прогулка по графу является некоей моделью дискретного марковского процесса (это словосочетание в статье часто встречается, поэтому и тут его нельзя было не упомянуть).
Подобный подход используется в других ранжирующих моделях на основе графа. Классический PageRank – лишь один из немногих алгоритмов, использующих данный принцип, и, при этом, он довольно ограничен. При ранжировании страниц целесообразно использовать как различные свойства их самих, так и свойства ссылок. Например, в реальности при вычислении PR учитывается, внешняя ссылка по отношению к сайту или внутренняя. Т.е. следующим этапом развития «графовых» методов стало использование свойств их вершин и ребер для ранжирования. В статье даны ссылки на различные работы, посвященные таким алгоритмам, но особо выделяется один – Semi-Supervised Page-Rank, который авторами работы назван передовым и современным. Эта технология использует десять свойств для ребер:
- тип ссылки (внутренняя или внешняя)
- количество входящих ссылок донора
- количество исходящих ссылок донора
- количество входящих ссылок акцептора
- количество исходящих ссылок акцептора
- уровень вложенности URL донора
- уровень вложенности URL акцептора
- длина URL донора
- длина URL акцептора
- вес (кратность) ребра (т.е. число ссылок, донор и акцептор которых совпадают с донором и акцептором данной ссылки).
Для каждого узла используются 5 свойств:
- количество входящих ссылок страницы
- количество исходящих ссылок страницы
- количество «двухшаговых» соседей страницы (число страниц, связанных с данной через две последовательные ссылки)
- уровень вложенности URL страницы
- длину URL страницы
Считается, что данные характеристики повышают качество (о том, как оно оценивается, будет сказано ниже) ранжирования по сравнению с PR. В частности, по оценке Normalized Discounted Cumulative Gain (NDCG) превосходство SSP составляет 0,8%.
Но авторы SNP в своей статье сетуют на то, что SSP не учитывает при ранжировании свойства соседних ребер вершин, полагая, что это могло бы добавить еще полпроцента прироста качества. Среди причин целесообразности учитывать свойства соседей называются следующие:
— Неравномерное распределение некоторых свойств страниц. Считается, что вершина с высоким весом должна иметь соседа с тоже высоким весом. А свойства соседей могут значительно отличаться. Например, если взять возраст страницы, то более старая вполне может иметь множество молодых соседок. Тогда, если учитывать дату создания документа, можно получить сильный перекос значений их конечных весов. Поэтому, по мнению авторов SNP, нужно «сглаживать» значения свойств между соседями.
— «Разреженность» данных. Информация, на основе которой определяются некоторые свойства вершин и ребер может быть неполной или неточной. В качестве примера приводятся поведенческие факторы. Если страница отображается в выдаче, но на невысоких местах, то кликов на нее производится значительно меньше по сравнению со страницами из топа, т.к. пользователи могут ее просто не заметить. Соответственно, данных, которые определяют свойства такой страницы, может быть недостаточно – возникает «разреженность».
— «Зашумленность» значений свойств, которая может вызывать скачки весов при переходе от одного соседа к другому. В качестве примера «зашумленности» приводится среднее число просмотров страницы, которую посетил несколько раз только один пользователь. Среднее, вычисленное по одному пользователю, не имеет смысла, а потому представляет собой «информационный шум».
Кроме того, авторы статьи в недостатки многих алгоритмов записывают отсутствие теоретического обоснования их моделей, отсутствие теоретически обоснованного метода обучения алгоритма, а также ограничения, которые не позволяют их использовать на широком классе задач. Все вышеуказанные недостатки они предлагают устранить в своем подходе – SNP. И им это, надо сказать, удается. И вот почему:
- Построенная ими модель представлена в общем виде, т.е. на ее основе можно решать очень широкий класс различных задач, а не только ранжирование веб-страниц. При этом в зависимости от настройки модели все описанные ранее подобные алгоритмы (в т.ч. и PR, и SSP) являются ее частными случаями. Это весьма красиво с научной точки зрения.
- Построенная ими модель учитывает не только собственные веса страниц и ссылок, но и свойства их «соседей». И если необходимость обеспечения «равномерности» распределения значений свойств среди соседей вызывает сомнения, то с точки зрения решения проблемы «разреженности» и «зашумленности» данных, этот подход показал высокую эффективность (судя по представленным результатам экспериментов).
- Для построенной модели предложен теоретически обоснованный алгоритм обучения, который оптимизирует целевую функцию (в данном случае – метрику качества ранжирования). Самое интересное, что для этого они использовали неплохой математический аппарат и смогли вычислить градиенты (производные) весов относительно настраиваемых параметров алгоритма. Если предыдущее предложение для вас является нагромождением непонятных слов, то просто поверьте на слово – это очень изящное решение.
Перед тем как перейти к рассмотрению сути SNP отметим, что в качестве примера одного из свойств страницы (ссылки), которые можно использовать для ранжирования, в статье приводится BM25. Т.е. на выходе такого алгоритма получается некий PR, зависящий от запроса. И хотя исследования такой модификации метода в статье не представлены, сама возможность такого использования PR весьма интересна.
Далее опустим «общий вид» модели и будем ее рассматривать исключительно для классического ранжирования ссылочного графа. Тогда главной особенностью SNP в такой постановке задачи становится учет свойств соседних вершин (ребер). Как это делается? Тоже весьма изящным способом.
Вернемся к описанному выше случайному блужданию по графу. Исходными данными для него являются начальные веса вершин (начальные вероятности) и веса ребер (вероятности переходов). Выходом алгоритма являются конечные веса вершин (стационарные вероятности). Авторы SNP предлагают «запустить» еще два случайных блуждания (или марковских процесса), которые являются как бы вложенными относительно уже рассмотренного ранее блуждания (отсюда и название алгоритма). Эти две независимые «прогулки» нужны для того, чтобы определить начальные веса вершин (первый марковский процесс) и веса ребер (второй марковский процесс). При случайном блуждании начальный вес как бы размазывается («сглаживается») по графу с учетом особенностей его структуры. В этом и заключается изящность решения, использованного авторами SNP: применить марковский процесс для «сглаживания» значений свойств страниц и ссылок. Если этот метод хорошо работает для «размазывания» конечных весов с учетом структуры графа, то он неплохо будет работать и на «размазывании» начальных весов.
Для демонстрации эффективности предложенного метода в конце статьи представлены результаты экспериментов. Для этого на основе коллекции документов, собранной в доменном пространстве «одной из крупнейших европейских стран» (2.52 миллиарда страниц и 21.12 миллиарда ссылок), был построен ссылочный граф. Для такой огромной размерности использовались параллельные вычисления (граф разбили на 700 частей). Далее было сформировано множество запросов (тоже по результатам работы в «одной из крупнейших европейских стран»). А для каждого запроса «профессиональными асессорами, нанятыми Яндексом» была проведена оценка релевантности ряда страниц по стандартной шкале: perfect, excellent, good, fair, bad. В сумме таким образом «разметили» 126,4 тысячи пар запрос-URL при 16,7 тысячах запросов. Из 90% оцененных пар сформировали обучающую выборку, из оставшихся 10% – тестовую. На первой обучали алгоритмы, на второй – тестировали. Отметим, что авторы SNP в недостатки статьи, посвященной SSP, записали использование ими оценок, построенных непосредственно на подсчете кликов: «Формат нашего экспериментального исследования более адекватен реальности и поисковой индустрии, нежели применяемый авторами SSP, которые оценивали документы тестовой выборки, используя бинарную шкалу релевантностей, и обучали SSP на зашумленных неявных оценках, построенных непосредственно на базе подсчетов кликов на документ». С появлением собственного хорошего алгоритма SNP клики оказались «шумными», хотя раньше неоднократно заявлялось, что «клики – наше всё» и «без кликстрима качественное ранжирование невозможно».
Для эксперимента в качестве свойств SNP использовались те же свойства, что и у SSP, и дополнительные «временные» свойства, учитывающие «возраст» страниц. Чтобы сделать возможной оценку качества на основе NDCG, ранжирование сделали запросозависимым, добавив к конечному весу страницы соответствующее значение BM25, умноженное на λ – обучаемый параметр модели.
Алгоритмы обучили: метод для SNP подошел и для SSP, т.к. последний является частным случаем первого, и прогнали по тестовой выборке, получив следующие результаты:
|
Тип свойств |
Итерация |
Метод |
NDCG@3 |
@5 |
|
SSP + [7] |
Первая |
SSP |
0.76326 |
0.79902 |
|
SNP |
0.76522 |
0.79964 |
||
|
SSP + [7] |
Последняя |
SSP |
0.76534 |
0.80007 |
|
SNP |
0.76909 |
0.80368 |
||
|
Временные |
Первая |
SSP |
0.76336 |
0.80208 |
|
|
SNP |
0.76432 |
0.80031 |
|
|
Временные |
Последняя |
SSP |
0.7688 |
0.80426 |
|
SNP |
0.77543 |
0.80753 |
Если смотреть исключительно на цифры, преимущество SNP гомеопатическое – максимально 0,8%. Однако авторы статьи пытаются доказать, что это существенно, ссылаясь на аналогичное превосходство SSP над PR.
Т.к. PR является частным случаем SNP, то в экспериментах обучили и его, определив оптимальный коэффициент затухания (α=0,9514) и получив очередное «существенное» улучшение на 0,35%. При этом коэффициент 0.95 означает, что только 5% посещений страниц заканчиваются кликами на ссылку, что, очевидно, не соответствует реальности. Но оптимизаторов качества ранжирования это не смущает.
А вот следующий эксперимент представляет определенный интерес. Для его проведения авторы сымитировали «разреженность» данных, выбросив часть свойств некоторых страниц. Результаты получились интересными. Посмотрим на графики ниже, на них представлены зависимости качества ранжирования от степени «разреженности» данных (r – доля страниц, у которых проредили свойства) для SSP, SNP и двух модификация SNP (SNP1, SNP2), суть которых для данного комментария не существенна.

Вот здесь преимущества SSP встают в полный рост – его устойчивость относительно «разреженности» данных очень высока, именно благодаря «сглаживанию» свойств между «соседями». Данный результат является одним из наиболее интересных.
Отдельно хочется подчеркнуть важный аспект, который выше упомянут лишь вскользь, а именно запросозависимость SNP. Это открывает массу новых возможностей использования модели. Если классический PR зависел только от «геометрии» графа, его некоторые модификации учитывали только внутренние свойства страниц и ссылок, не зависящие от внешних условий, то SNP представляет собой PageRank, который позволяет выполнять ранжирование с учетом запроса. Если рассмотреть классическую поисковую задачу: отсортировать страницы по убыванию их релевантности относительно запроса, то ее можно решить при помощи только SNP, введя в качестве одного из свойств страницы или даже ссылки запросозависимую характеристику на базе BM25. Ранжирование будет проведено не только с учетом структуры ссылочного графа, но и содержания страниц и анкоров с точки зрения их релевантности запросу.
В завершение отметим, что с научной точки зрения SNP является новаторским и довольно мощным методом ранжирования на основе графа. Найдет ли он применение на практике – покажет время.
Еще по теме:
- Что делать, если резко просел трафик с Яндекса? Пошаговая инструкция по диагностике причин Прежде всего, важно правильно определить тип просевшего трафика, после чего можем перейти к анализу причин его падения. Что делать дальше и в каком случае –...
- Отмена ссылочного ранжирования в Яндекс. Взгляд из-за бугра Арвид Линд (Arvid Linde), независимый SEO-консультант, после отмены ссылочного ранжирования проанализировал выдачу Яндекса в нескольких популярных тематиках (недвижимость, SEO, похудение). Определив, какие сайты выпали из...
- SEO-гайд для новичков: анализ просадки позиций в Яндексе Порой падение позиций в Яндексе бывает резким, а иногда просадка происходит медленно, но верно. В этой статье мы расскажем, как по характеру просадки позиций выявить...
- Как настроить Google Analytics: отвечаем на частые вопросы Отвечаем на часто задаваемые вопросы по настройке Google Analytics: создание и настройка событий и целей, отслеживание 404 ошибки, рефспам и его влияние, разделение органического трафика, создание групп...
- ТОП тематик, которые выросли и просели из-за коронавируса В статье рассмотрим ТОП тематик интернет-ресурсов, которые просели и выросли в связи с коронавирусом (COVID-19), основываясь на собственных наблюденях и результатах глобального исследования компании SimilarWeb....
Есть вопросы?
Задайте их прямо сейчас, и мы ответим в течение 8 рабочих часов.


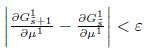 , то на выход
, то на выход 

 (6 оценок, среднее: 4,83 из 5)
(6 оценок, среднее: 4,83 из 5)

А скажите, где оригинал можно найти?
Анна, мы брали оригинал статьи здесь.
Скажите пожалуйста, при настройке внутренней перелинковки, есть ли необходимость закрывать от индексации сквозные ссылки меню?! И каким именно способом вообще лучше закрывать ссылки, от индексации, дабы не расплескивать вес на "ненужные" страницы? Спасибо.
Имеет смысл, но не во всех случаях. Если у магазина большое меню и его содержание в разы превышает основной контент посадочной страницы, то лучше такое меню спрятать. Но при этом важно помнить, что меню несет и навигационную роль. Поэтому просто взять и убрать его на всех страницах неправильно. В каждом случае нужно смотреть индивидуально. Если меню не сильно объемное, то закрывать его не нужно.
По поводу веса – на него сейчас неправильно ориентироваться. Перелинковка должна быть естественной: цепочки ссылок, популярные товары, другие товары этой категории.
Александр, спасибо за ответ, но если я вас правильно понял, то вес страницы играет не самую фатальную роль, лучше ориентироваться на поведентческий фактор внутри сайта?!
НО тем не менее, когда присутствует ситуация, где с каждой страницы с товаром идут необходимые ссылки из текста на "контакты", "условия оплаты и доставки" … это ведь приводит к потере веса страницы, и непотребному приобретению гигантского веса страницы реципиентов (даже при условии того, что они находятся на этом же сайте).
Не логичнее было бы закрыть в тексте такие ссылки от индексации? И как?! (достаточно ли будет noindex или все таки нужен будет использовать js? )
Верно, лучше ориентироваться на поведенческие внутри сайта. Работать над весом без оглядки на другие моменты неверно.
Вы сами пишете, что "с каждой страницы с товаром идут НЕОБХОДИМЫЕ ссылки из текста на "контакты", "условия оплаты и доставки". Отсутствие этой действительно важной при покупке информации — минус к коммерческим факторам ранжирования.
Тет noindex понимает только Яндекс. Поэтому если что-то скрывать, то лучше использовать другой способ.
Оптимизация весов с помощью перелинковки увеличивает общий тематический трафик на сайт не на какие-то проценты, а в разы. 🙂
Поэтому ориентироваться на перелинковку — правильно. 🙂
Тут никаких общих правил, типа "закрыть меню" или "линковать по такой-то схеме" не существует, потому что они все не верны и в среднем скорее ухудшают ситуацию. Это правила простецкого олдскульного СЕО, которые работали очень давно. По статье выше видно, на каком уровне математики работает сегодня Яндекс, современный сеошник должен работать на похожем. 🙂
При перелинковке давно уже нужно считать, а не тупо линковать. Нужно выбрать какую-то метрику для расчёта итога перелинковки и оптимизировать её значение. На двух идентичных по структуре сайтах с разными наборами запросов правила перелинковки могут принципиально отличаться.
Вам нажно сделать лайки к коментариям))) но за отсутсвием онного, просто скажу Спасибо за ответ )))
Можно как пример, какой-либо метрики для расчета при перелинковке?
У нас была по этому поводу статья, которую так и не удосужились опубликовать. 🙂
И был доклад на Ашмановке-2013, даже видео ещё живо: https://live.digitaloctober.ru/embed/2490#time1386242480. Лектор из меня тот ещё, но что-то понять наверное можно. 🙂
Спасибо за ссылку на доклад.
Но, если я не знаю алгоритм вычисления PR в Яндексе — и Вы говорите, что он отличается от классического (в этом и сомнений особо нет, столько воды с тех пор утекло), то получается я и не могу оптимизировать никакую функцию. Разве что кроме вымышленной 🙂
>Вы говорите, что он отличается от классического (в этом и сомнений особо нет, столько воды с тех пор утекло), то получается я и не могу оптимизировать никакую функцию Тут такой расклад на сегодня. Мы с тех пор провели несколько экспериментов по оптимизации на классическом алгоритме пэйджранка, на средних сайтах, примерно по 10К индексируемых документов. Результаты получились немного похуже, чем с "более правильными" алгоритмами, но всё равно отличные. И они однозначно говорят о том, что такую оптимизацию стоит делать.
постеснялся еще раз спрашивать, но если уж JohnGalt спросил, то я тоже поддерживаю и с удовольствием посмотрел бы на пример метрики! Спасибо
Хотелось бы узнать мнение Ильи Зябрева по следующим возникшим вопросам: Какую роль алгоритм SNP играет в контексте Matrixnet'a? Можно ли сказать, что на основе алгоритма вычисляется еще один фактор для документа, который затем участвует в ранжировании по полученному на основе матрикснета алгоритму? И этот показатель из разряда "чем выше, тем лучше"?
Если Илья, при ответе, еще и обьяснит для остальных что такое "контекст matriksnet'а", было бы вообще замечательно ))
SNP это не "ещё один фактор" Матрикснета, а метод для вычисления факторов. Например, с его помощью можно вычислять PageRank или BrowseRank. Если его начнут применять для вычисления PR, то значение этого фактора для СЕО резко возрастёт, т.к. вырастет кореляция PR с выдачей по большинству частотных запросов и вырастет "аблолютная сила" этого фактора.
Что касается по-запросного PR с учётом BM25, то внедрение его не очевидно, ввиду большой вычислительной сложности. Но в случае внедрения резко повысится значение анкоров и доноров, релевантных нужному запросу. Не тематичных, а именно релевантных по BM25, т.е. с большим % вхождения конкретных слов запроса в текст.
Илья, благодарю за ответ! Почаще бы публиковались для обычных смертных 🙂