Как Google может оценивать сайты. Новая модель Knowledge-Based Trust (КВТ)

1. ВВЕДЕНИЕ

“Обучение доверию — одна из наиболее трудных задач жизни” – Исаак Уоттс.

Качественная оценка веб-страниц имеет огромное значение для сетевого поиска. Традиционно для этой задачи использовались внешние данные, такие, как гиперссылки или история просмотров. Однако такие данные главным образом отображают популярность страницы. Например, сайты сплетен, перечисленные в [16], в основном, имеют высокие значения PageRank [4], но при этом их нельзя считать надежными. С другой стороны некоторые менее популярные веб-сайты, тем не менее, содержат очень точную информацию.

В этой статье мы рассматриваем фундаментальную задачу оценки достоверности веб-ресурсов. Фактически мы определяем достоверность или точность страницы как вероятность того, что она содержит факт, соответствующий действительности (например, национальность Барака Обамы), независимо от количества его упоминаний. Таким образом, мы не штрафуем ресурсы, содержащие малое количество фактов до тех пор, пока они достоверны.

Мы предлагаем использовать KBT, чтобы оценивать достоверность страницы следующим образом. Мы собираем факты со многих веб-ресурсов, используя методы парсинга. Далее мы совокупно оцениваем достоверность этих фактов и соответствующих страниц, используя выводы, основанные на вероятностной модели. Процесс такого анализа — итеративный, так как страница считается достоверной, если достоверны размещенные на ней факты, и факты заслуживают доверия, если его заслуживает и их источник. Кроме того, в статье мы покажем, как запустить итеративный процесс оценки точности веб-страниц, так, чтобы обеспечить его сходимость. Метод парсинга фактов, который мы применяем, основан на проекте KV (Knowledge Vault – хранилище знаний) [10]. KV использует 16 различных технологий парсинга, чтобы извлекать «триплеты знаний» (субъект, предикат, объект) из веб-страниц. Пример такого триплета (Барак Обама, национальность, США). Объект — это реальная сущность, имеющая идентификатор (ID), например, MID (Machine ID) в базе знаний Freebase [2]; предикат — предопределяется в базе знаний (Freebase) и описывает некоторое свойство субъекта; объект может быть сущностью, символьной строкой, численным значением или датой.

Факты, спарсенные на основе методов, подобных KV, могут быть ложными. Один из методов оценки их достоверности описан в [11]. Однако в данной работе не делается отличий между фактическими ошибками на странице и ошибками, допущенными при парсинге данных. Как показано в [11], ошибки парсинга встречаются гораздо чаще по сравнению с фактическими. Поэтому игнорирование данного различия может привести к неправильной оценке достоверности сайта.

Другая проблема подхода, представленного в [11], заключается в том, что он оценивает надежность каждой страницы независимо. Это может вызвать проблемы, когда данных мало. Например, более чем для одного миллиарда страниц KV может спарсить только один триплет, что помешает адекватно оценить их достоверность. С другой стороны, для некоторых страниц KV парсит десятки тысяч триплетов, что может создать проблемы с вычислительной точки зрения.

Метод KBT, предлагаемый в этой статье, решает некоторые из озвученных проблем. Во-первых, мы представляем более сложную вероятностную модель, которая умеет различать два главных типа ошибок: ошибочные факты на страницах и ошибки, совершенные при парсинге. Это обеспечивает намного более точную оценку достоверности веб-ресурсов. Мы предлагаем эффективный, настраиваемый алгоритм для проведения анализа и параметрической оценки на основе предложенной вероятностной модели (Раздел 3).

Во-вторых, мы предлагаем метод, позволяющий избегать ошибок, связанных с количеством фактов на страницах. В частности, страницы, которые содержат малое количество триплетов, «склеиваются» с другими документами этого же сайта. Страницы с большим числом триплетов, наоборот, разбиваются на меньшие по количеству фактов документы, чтобы избежать проблем, связанных с вычислительной сложностью (Раздел 4).

В-третьих, в данной статье представлена подробная, крупномасштабная оценка предлагаемой модели. В частности, мы спарсили 2.8 миллиарда фактов-триплетов, чтобы оценить достоверность 119 миллионов страниц и 5.6 миллионов сайтов (Раздел 5).

Подчеркнем, что достоверность ресурсов является дополнительной характеристикой для оценки их качества. В разделе 5.4.2 обсуждаются новые возможности метода с целью его улучшения и использования совместно с уже существующими оценками, такими, как PageRank. Кроме того, отметим, что хотя в данной статье метод представлен в контексте синтеза знаний, в общем виде он может использоваться для более широкого класса задач, например, связанных с интеграцией и выборкой данных.

2. ПОСТАНОВКА И ОБЗОР ЗАДАЧИ

Данный раздел мы начнем с формального определения оценки достоверности, основанной на базе знаний (KBT). Затем мы проведем краткий обзор нашей предыдущей работы, которая решает связанную с данной задачу синтеза знаний [11]. В завершении мы представим обзор нашего подхода и укажем отличия от предыдущей работы.

2.1 Постановка задачи

Пусть имеется множество веб-ресурсов W и множество экстракторов E. Экстрактор — метод парсинга триплета (субъект, предикат, объект) с интернет-страниц. Например, один экстрактор может искать паттерн “$A, президент $B…”, из которого извлекается триплет (A, национальность, B). Естественно, это не всегда корректно (например, если A — президент компании, а не страны). Кроме того, экстрактор переводит символьные обозначения сущностей (например, названия) в их идентификаторы, такие, как MID в Freebase, и иногда при этом возникают ошибки. Данные ошибки являются одним из предметов наших исследований и мотивом для написания данной статьи.

Ниже мы представим такой триплет в виде пары (данные, значение), где данные — это форма представления (субъект, предикат), которая описывает свойство сущности, а объект представляет собой его значение. Совокупность основных обозначений, используемых в данной статье, представлена в таблице 1.

Таблица 1: Основные обозначения, используемые в данной статье

Обозначение	Описание
w∈W	Веб-страница
e∈E	Экстрактор
d	Данные
v	Значение
Xewdv	Бинарный индикатор того, что e спарсил (d,v) из w
Xwdv	Все «извлечения» (d,v) из w
Xd	Все данные о d
X	Все входные данные
Cwdv	Бинарный индикатор того, что w содержит (d,v)
Tdv	Бинарный индикатор того, что v правильное значение d
Vd	Истинное значение d при условии единственности правильного значения
Aw	Точность (достоверность) страницы w
Pe;Re	Оценки precision и recall для экстрактора e

Определим переменную наблюдения X_ewdv. Пусть X_ewdv = 1, если экстрактор e извлек значения v для данных d из веб-страницы w; в противном случае — X_ewdv = 0. Экстрактор также может определять значения вероятности того, что спарсенные данные достоверны. Данное расширение метода будет рассмотрено в Разделе 3.5. Используем матрицу X = {X_ewdv}, чтобы обозначить все данные.

Представим X как «куб данных», как показано на рисунке 1 (b). Таблица 2 показывает пример горизонтального «сечения» этого куба для случая, когда d = (Барак Обама, национальность). Рассмотрим этот пример подробнее.

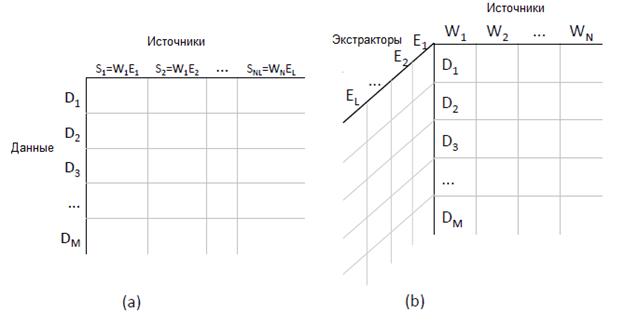
Рисунок 1: Форма входных данных для (a) однослойной модели и (b) многослойной модели.

Таблица 2. Национальность Обамы, спарсенная пятью экстракторами с восьми веб-страниц

	Value	E1	E2	E3	E4	E5
W1	USA	USA	USA	USA	USA	Kenya
W2	USA	USA	USA	USA	N.Amer.
W3	USA	USA		USA	N. Amer.
W4	USA	USA		USA	Kenya
W5	Kenya	Kenya	Kenya	Kenya	Kenya	Kenya
W6	Kenya	Kenya		Kenya	USA
W7	—			Kenya		Kenya
W8	—					Kenya

ПРИМЕР 2.1. Предположим, что у нас есть 8 интернет-страниц, W₁ — W₈, и нас интересуют данные (Обама, национальность). Значения для этих данных, которые содержит каждая из интернет-страниц, представлены в первом столбце Таблицы 2. Как видно W₁ — W₄ указывают США как национальность Обамы, тогда как W₅ — W₆ – Кению (ложное значение). Страницы W₇ — W₈ не предоставляют информации относительно национальности Обамы.

Теперь предположим, что у нас есть 5 различных экстракторов с различной надежностью. Значения, которые они извлекают для указанных данных из этих 8 интернет-страниц, представлены в таблице. Экстрактор E₁ парсит все представленные триплеты правильно. Экстрактор E₂ пропускает некоторые триплеты (ложные отрицания), но все его «извлечения» верны. Экстрактор E₃ извлекает триплеты, но при этом неправильно определяет значение Кения со страницы W₇, при том, что на W₇ не упоминается данный факт (ложное подтверждение). Экстракторы E₄ и E₅ имеют низкое качество парсинга, пропуская триплеты и допуская ошибки.

Для каждой веб-страницы w ∈ W определим ее точность (достоверность) А_w, как вероятность того, что факты, представленные на ней (значения данных), верны (т.е. соответствуют действительности). Тогда A={A_w} множество точностей всех страниц. Сформулируем задачу оценки KBT.

ОПРЕДЕЛЕНИЕ 2.2 (ОЦЕНКА KBT). Задача оценки KBT заключается в том, чтобы оценить точность веб-страниц A={A_w}, заданную над матрицей наблюдения X = {X_ewdv} спарсенных триплетов.

2.2 Оценка достоверности на основе однослойной модели

Оценка KBT тесно связана с проблемой синтеза знаний, которую мы исследовали в нашей предыдущей работе [11] и в которой оцениваются истинные (но неявные) значения данных с учетом зашумления наблюдений. Мы ввели бинарные неявные переменные T_dv, которые показывают, является ли v правильным значением для данных d. Пусть T = {T_dv}. Зададим матрицу наблюдения X = {X_ewdv}, тогда задача синтеза знаний заключается в вычислении последующих данных на основе неявных переменных p (T|X).

Один из способов решения данной проблемы заключается в том, чтобы «сжать» куб данных в двумерную матрицу, как показано на рисунке 1 (a), рассматривая каждую пару веб-страницы и экстрактора как отдельный источник информации. При таком подходе данные представляются в виде, для обработки которого существует множество стандартных методов [22]. Мы называем это однослойной моделью. Рассмотрим ее подробнее и позже проведем ее сравнение с новой моделью.

В [11] мы использовали вероятностную модель, описанную в [8]. Мы предполагаем, что у данных может быть одно единственное истинное значение. Это предположение справедливо для функциональных предикатов, таких, как национальность или дата рождения, но недействительно для предикатов с множеством значений, например, ребенок. Тем не менее, в [11] на основе экспериментальных данных показано, что предположение о единственности истинного значения дает хорошие результаты на практике даже для нефункциональных предикатов, поэтому в данной работе для простоты будем также его использовать. В [27, 33] представлены методы для многозначных данных.

На основе предположения о единственности истинного значения определим неявную переменную V_d∈dom(d), чтобы представить истинное значение для d, где dom(d) область значений d. Пусть V = {V_d}, тогда можно вывести T = {T_dv} из V на основе «единственности истинного значения». Определим следующую модель наблюдения:

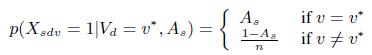(1)

где v* — истинное значение, s = (w; e) — источник, A_s∈[0; 1] — точность этого источника данных и n — число ложных значений для области определения d (т.е. мы принимаем |dom(d)| = n + 1). Согласно модели, вероятность того, что s содержит истинное значение v для d является точностью, тогда как вероятность того, что s содержит одно из n ложных значений равна 1-A_s, деленное на n.

Для данной модели можно использовать теорему Байеса и вычислить p(V_d|X_d,A), где X_d = {X_sdv} — все данные, имеющие отношение к d (т.е., d-й ряд матрицы наблюдения), A = {A_s} — множество всех значений точности. Полагая, что распределение p(V_d) равномерное, можно записать:

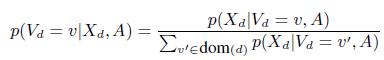 (2)

где функция вероятности может быть получена из Уравнения (1), с учетом независимости источников данных:

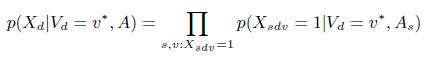(3)

Эта модель называется ACCU [8]. Немного более продвинутая модель, известная, как POPACCU, использует неравномерное распределение ложных значений, а эмпирическое распределение, построенное на основе наблюдаемых данных. Было доказано, что модель POPACCU — монотонная, т.е. добавление большего количества источников не ухудшает качество результатов [13].

И в ACCU, и в POPACCU необходимо оценивать совокупность неявных значений V = {V_d} и параметры точности A = {A_s}. Итеративный алгоритм, подобный EM-алгоритму, для решения данной задачи был предложен в [8]:

1. Установить счетчик итераций t=0.

2. Задать некоторое значение параметра A^t_s (например, 0.8).

3. Оценить p(V_d|X_d, A_s) параллельно для всех d, используя Уравнение (2). На основе этого можно вычислить наиболее вероятное значение  (Стадия Е алгоритма)

4. Оценить  по формуле:

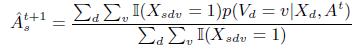(4)

где I(a= b)=1, если a= b, и 0 в противном случае. Согласно данному уравнению, оценка точности источника производится на основе средней вероятности его фактов (Стадия М алгоритма).

5. Переход к шагу 3. Итерации повторяются до выполнения условия останова.

Теоретические свойства этого алгоритма описаны в [8].

2.3 Оценка KBT c использованием многослойной модели

Хотя оценка KBT тесно связана с синтезом знаний, однослойная модель имеет две существенные проблемы. Во-первых, невозможность оценить достоверность веб-страниц независимо от экстракторов. A_s — это точность пары (w; e), а не точность самой страницы. Простое использование всех значений источника, очевидно, не будет работать. В частности, в нашем примере с Обамой можно сделать неправильный вывод о том, что W₁ — плохой источник при возникновении ошибки парсинга.

Во-вторых, на основе однослойной модели нельзя адекватно оценить достоверность триплетов. В нашем примере есть 12 источников (т.е., пар страница-экстрактор) для США и 12 источников для Кении. Т.е. можно сделать вывод, что США и Кения равновероятны, однако на самом деле это не так: экстракторы E₁ — E₃ «соглашаются» друг с другом, а потому являются более надежными. Поэтому значение «Кения», спарсенное E₄ — E₅, и которое согласно однослойной модели является более вероятным, чем «США», на самом деле объясняется ошибками парсинга.

Для решения данных проблем необходимо отличать ошибки парсинга от ошибок источников. В нашем примере требуется различать правильно спарсенный истинный триплет (например, США от W₁ — W₄), правильно спарсенный ложный триплет (например, Кения от W₅ — W₆), неправильно спарсенный верный триплет (например, США от W₆) и неправильно спарсенный ложный триплет (например, Кения от W₁; W₄; W₇-W₈).

В этой статье мы представляем новую вероятностную модель, которая позволяет оценить точность каждой веб-страницы, выведя за рамки задачи шум, вносимый экстракторами. Она имеет два существенных отличия от однослойной модели. Во-первых, в дополнение к неявным переменным, необходимым для представления истинных значений данных (V_d), в новой модели вводится множество неявных переменных для идентификации того, было ли каждое «извлечение» правильным или нет, что позволяет отличать ошибки парсинга от ошибок исходных данных. Во-вторых, вместо использования для точности пар (e; w) в новой модели определяется множество параметров для точности веб-страниц и качества экстракторов, что позволяет отделять качество страниц от качества экстракторов. Новая модель называется многослойной, потому что содержит два множества неявных переменных и параметров (Раздел 3).

Принципиальные преимущества многослойной модели над однослойной позволяют получить адекватную оценку KBT. В Разделе 4 будет показано, как в динамике выбрать «степень детализации» веб-страниц и экстракторов, а в Разделе 5 — насколько оба компонента важны с точки зрения улучшения качества работы однослойной модели.

3. МНОГОСЛОЙНАЯ МОДЕЛЬ

В этом разделе подробно описывается процесс вычисления А = {A_w} на основе матрицы наблюдения X = {X_ewdv} с использованием многослойной модели.

3.1 Многослойная модель

Расширим предыдущую однослойную модель по двум направлениям. Во-первых, введем двойные неявные переменные C_wdv, которые определяют, содержит ли веб-страница w триплет (d; v) или нет. Аналогично уравнению (1) зависимость этих переменных от истинных значений V_d и точности каждой страницы А_w определяется следующим образом:

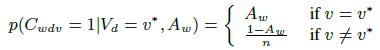 (5)

Во-вторых, согласно [27, 33] мы используем двухпараметрическую шумовую модель для наблюдаемых данных:

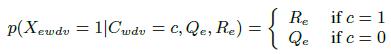(6)

Здесь R_e — оценка recall экстрактора, то есть, вероятность парсинга существующего триплета. И Q_e=1 — specifity, т.е. вероятность парсинга несуществующего триплета. Параметр Q_e связан с recall (R_е) и precision (P_e) следующим образом:

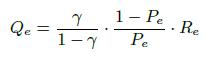 (7)

где  для любого , как показано в [27]. В таблице 3 представлен пример вычисления Q_e на основе P_e и R_e.

Чтобы закончить описание модели, необходимо определить априорную вероятность ее различных параметров:

 (8)

Для простоты используем равномерное распределение параметров. По умолчанию устанавливаются следующие значения А_w = 0.8, R_е = 0.8 и Q_e = 0.2. В Разделе 5 обсуждается альтернативный способ оценки начальных значений А_w, основанный на выборке правильных триплетов данной страницы с использованием внешних оценок правильности (Freebase [2]).

Пусть V = {V_d}, C = {C_wdv} и Z = (V; C) — все неявные переменные. Тогда модельное распределение можно представить в виде:

(9)

На рисунке 2 представлена структура многослойной модели. Заштрихованный узел — наблюдаемые переменные; незаштрихованные узлы — неявные переменные или параметры. Стрелки указывают на зависимость между переменными и параметрами. Прямоугольниками представлена вложенность переменных и параметров.

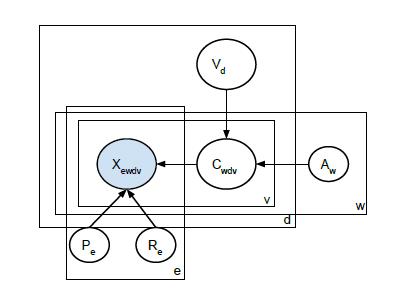
Рисунок 2. Графическое представление многослойной модели

3.2 Анализ

Recall, оценивающий KBT, требует вычисления апостериорных вероятностей p(A|X). Данная операция имеет высокую вычислительную сложность из-за неявных переменных Z. Один из методов решения данной проблемы – использование метода Монте-Карло по схеме Гиббса, например как в [32]. Однако для размерности данных, которые мы используем в данной статье, даже распределенные вычисления по данному методу могут быть медленными.

Более быстрой альтернативой является EM-алгоритм, который вычисляет точечные оценки всех параметров . Так как мы используем равномерное распределение, то это эквивалентно оценке максимального правдоподобия . На основе этого мы можем вывести .

Как показано в [26], EM-алгоритм имеет квадратичную сложность даже на однослойной модели, а потому не применим для данных веб-масштаба. Поэтому мы используем итеративную процедуру оценки, подобную EM-алгоритму, в которой сперва инициализируются параметры, как описано ранее, а затем чередуются вычисления оценок Z и θ до выполнения условия сходимости.

Проведем предварительный обзор данного алгоритма, представив дополнительные подробности в последующих разделах.

В нашем случае Z состоит из двух «слоев» переменных. Мы вычисляем их последовательно следующим образом. Во-первых, пусть X_wdv = {X_ewdv} — все результаты парсинга со страницы w триплета t = (d; v). Определяем правильность парсинга  по методу, представленному в Разделе 3.3.1, затем вычисляется , которая является наилучшим предположением об «истинном содержании» каждой страницы. Это можно реализовать параллельно по d, w и v.

Пусть  — все оцененные значения d для различных страниц. Вычисления  производятся в последовательности, представленной в Разделе 3.3.2, и затем вычисляется , которая является наилучшим предположением об «истинных значениях» данных. Это может быть реализовано параллельно по d.

После оценки неявных переменных можно вычислить . Данная операция проводится в 2 этапа (однако может быть реализована параллельно): оценка исходной точности {A_w} и надежности экстрактора {P_e; R_е} в последовательности, представленной в Разделе 3.4.

В Алгоритме 1 представлен псевдокод данного подхода.

Алгоритм 1: MULTILAYER(X; t_max)

Вход: X: все спарсенные данные; tmax — максимальное число итераций.

Выход: оценки Z и θ.

1 Инициализия значениями по умолчанию;

2 for t=[1; t_max] do

3 Оценка C по формулам (15, 26, 31);

4 Оценка V по формулам (23-25);

5 Оценка θ₁ по формуле (28);

6 Оценка θ₂ по формулам (32-33);

7, если Z; θ сходятся, тогда

8 Стоп;

9 Возврат Z; θ;

3.3 Оценка неявных переменных

Ниже детализированно рассмотрены методы оценки неявных переменных Z.

3.3.1 Оценка правильности парсинга

Рассмотрим вычисление p(C_wdv = 1|X_wdv) в [27]. Обозначим априорную вероятность p (C_wdv = 1) как α. На начальных итерациях устанавливаем α = 0.5. Отметим, что при помощи фиксации априорной вероятности, мы разрываем связь между C_wdv и V_d в графической модели (рисунок 2). Таким образом, в последующих итерациях мы повторно оцениваем p(C_wdv = 1) с использованием результатов V_d, полученных из предыдущей итерации, как показано в Разделе 3.3.4.

На основе теоремы Байеса получим:

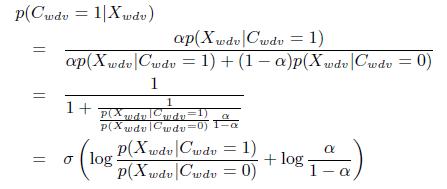(10)

где  — сигмоидальная функция.

Полагая, что экстракторы независимы, и используя Уравнение (6), вычислим соотношения вероятностей:

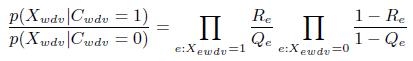(11)

Т.е. для каждого экстрактора мы можем вычислить метрику присутствия Pre_e для спарсенных триплетов и метрику отсутствия Abs_e для неспарсенных триплетов:

Для каждого триплета (w; d; v) мы можем вычислить его значимость как сумму метрик присутствия и отсутствия:

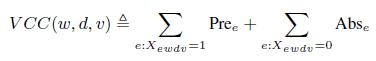 (14)

Соответственно, мы можем переписать Уравнение (10) следующим образом.

 (15)

ПРИМЕР 3.1. Рассмотрим экстракторы в примере, представленном в Таблице 2. Предположим, что мы знаем Q_e и R_e для каждого экстрактора e как показано в Таблице 3. Тогда мы можем вычислить Pre_e и Abs_e. Отметим, что в целом экстрактор с низким Q_e (маловероятный для парсинга несуществующего триплета, например, E₁, E₂) часто имеет большую метрику присутствия, а экстрактор с высоким Р_е (маловероятный для существующего триплета, например E₁, E₃) часто имеет малую (отрицательную) метрику отсутствия. При этом у низкокачественного экстрактора (например, E₅) зачастую малая метрика присутствия и большая метрика отсутствия.

Таблица 3. Качество и метрики экстракторов для примера из таблицы 2.

Теперь по формуле (15) вычислим вероятность того, что часть страниц имеет триплет t*=(Обама, национальность, США) с учетом α = 0.5. Для страницы W₁ видно, что экстракторы E₁ — E₄ спарсили t* так, что суммарная метрика равна (4.6 + 3.9 + 2.8 + 0.4) + (0) = 11.7 и, следовательно, p(C_1,t*=1 |X_w,t*) = σ(11.7) = 1. Для источника W₆ видно, что только E₄ спарсил t* так, что, суммарная метрика равна (0.4) + (- 4.6-0.7-4.5-0) = -9.4 и, следовательно, p(C_6,t*=1|X_6,t*)) = σ(-9.4) = 0. Другие значения для p(C_wt = 1|X_wt) представлены в Таблице 4.

Таблица 4: Распределение «правильности» парсинга и значений параметров на основе данных Таблиц 2,3.

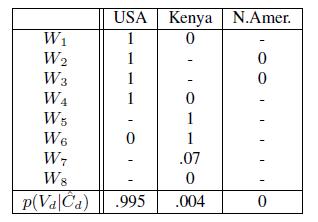
Вычислив p (C_wdv = 1|X_wdv), мы можем вычислить . Эти данные являются исходными для следующей стадии анализа.

3.3.2 Оценка истинного значения данных

На этой стадии мы вычисляем  на основе модели «единственности правды» [8]. По теореме Бейеса имеем:

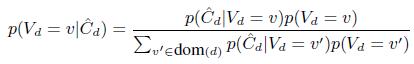(16)

Так как мы не имеем каких-либо предварительных знаний о правильных значениях, принимаем равномерное априорное распределение p(V_d = v). На основе уравнения (5) получим:

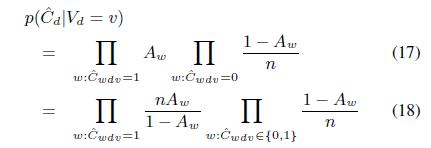
Начиная с последнего значения , постоянного относительно изменений v, можно опускать его вычисления.

Далее определяем значимость страниц:

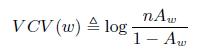(19)

По совокупности страниц, на которых представлены триплеты, определяем:

(20)

С учетом этого перепишем Уравнение (16) в виде:

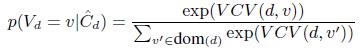(21)

ПРИМЕР 3.2. Предположим, что мы правильно определили для каждой страницы, на которой представлен триплет, значение, которое содержится во втором столбце Таблицы 2. Предположим, что каждый источник имеет точность А_w = 0.6 и n = 10, тогда их значимость равна . В этом случае значимость США равна 2.7*4 = 10.8, а значимость Кении — 2.7*2 = 5.4. У несуществующего значения, такого, как NAmer, значимость равна 0. Так как область определения содержит 10 ложных значений, то мы имеем 9 несуществующих значений. Следовательно, , где . Аналогично . Данные результаты представлены в последнем ряду Таблицы 4. Недостающая часть суммы полной вероятности 1-(0.995+0.004) равномерно распределена между оставшимися 9-ю значениями, которые не наблюдались, но представлены в области определения.

3.3.3 Улучшенная процедура оценки

До сих пор мы считали, что сперва необходимо вычислять оценку максимальной апостериорной вероятности , которую затем используем для определения V_d. Однако такой подход не учитывает погрешности . Более правильным будет вычислять на ее основе p(V_d|X_d).

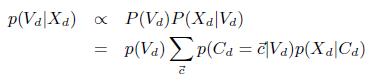 (22)

Здесь  определяетя как множество, где каждый элемент c_wdv указывает, содержит ли страница w триплет (d; v) (значение 1) или нет (значение 0).

На основе простой эвристической аппроксимации данного подхода заменим предыдущий подсчет значимости его взвешенной версией:

(23)

 

(24)

Тогда:

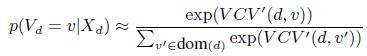(25)

Ниже покажем, что улучшенная процедура оценки снижает влияние погрешности вычисления  в экспериментах (Раздел 5.3.3).

3.3.4 Переоценка априорной вероятности

В Разделе 3.3.1 мы предположили, что  известна, что разрывает связь между V_d и C_wdv. Таким образом, мы обновляем эту априорную вероятность на каждой итерации в соответствии с правильностью фактов и точностью страницы:

 (26)

Тогда можно использовать дополненную оценку на следующей итерации. Рассмотрим данный процесс на примере.

ПРИМЕР 3.3. Рассмотрим вероятность того, что W₇ содержит t₀ = (Обама, национальность, Кения). Два экстрактора спарсили t₀ из W₇, и оценка значимости равна -2.65, таким образом, первоначальная оценка — . Однако после окончания предыдущей итерации p(V_d = Кения|X) = 0.04. Таким образом, мы можем переоценить априорную вероятность: , принимая А_w = 0.6. Следовательно, обновленная апостериорная вероятность , что меньше, чем ранее.

3.4 Оценка качества.

После оценок неявных переменных перейдем к оценкам параметров модели.

3.4.1 Качество источника

Следуя [8],оценим точность страницы, вычисляя среднюю вероятность представленных на ней фактов, являющихся истинными:

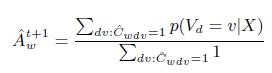 (27)

Принимая во внимание погрешность оценки , получим:

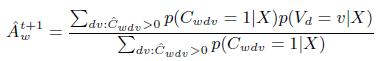 (28)

Это — ключевое уравнение KBT, позволяющее вычислить оценку точности веб-страницы как средневзвешенную вероятность фактов, которые она содержит. Веса равны вероятностям того, что данные факты представлены на странице.

3.4.2 Качество экстрактора

Согласно определениям precision и recall, мы можем оценить их следующим образом:

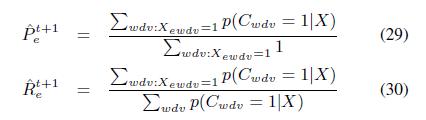
Отметим, что согласно представленным доказательствам в [27], существенно надежнее оценить P_e и R_e на основе данных, а затем по формуле (7) вычислить Q_e, по сравнению с непосредственной оценкой Q_e.

3.5 Использование вероятности успешности парсинга

До сих пор мы считали, что каждый экстрактор возвращает бинарное значение, отображающее информацию о том, «извлек» ли он триплет или нет X_ewdv={0; 1}. Однако в реальной жизни, экстракторы оценивают результат операции в виде вероятности того, что триплет присутствует на странице — мера уверенности. Обозначим данный вес как . Простым способом анализа таких данных является их бинаризация на основе пороговой обработки. Однако при этом теряется информация, что показано в следующем примере.

ПРИМЕР 3.4. Рассмотрим случай, когда E₁ и E₃ не полностью уверены относительно их парсинга W₃ и W₄. В частности E₁ оценивает каждое «извлечение» как успешное с вероятностью (т.е. уверенностью) 0.85, а E₃ — 0.5. Хотя ни у одного экстрактора нет полной уверенности, после совокупного анализа результатов их парсинга можно сказать, что W₃ и W₄ действительно содержат триплет T = (Обама, национальность, США). Однако, если используем пороговую обработку с отсечкой на уровне 0.7, то парсинг E₃ будет проигнорирован, что в итоге привет к выводу о том, что W₃ и W₄ не содержат заданный триплет. Далее США представлен в W₁ и W₂, а Кения — в W₅ и W₆, учитывая, что у всех страниц одинаковая точность, обе страны будут иметь равные вероятности того, что они являются истинной национальностью Обамы.

На основе аналогичного уравнению (23) подхода внесем изменения в уравнение (14):

(31)

Точно так же мы изменим оценки precision и recall:

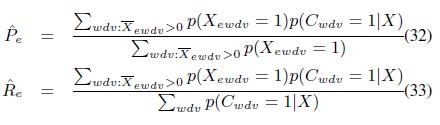
4. ДИНАМИЧЕСКИЙ ВЫБОР СТЕПЕНИ ДЕТАЛИЗАЦИИ

В данном разделе описывается технология выбора степени детализации веб-страниц. В конце раздела обсуждается ее использование для экстракторов. Данная стадия является подготовительной для многослойной модели.

В идеале — использовать наивысшую степень детализации. Например, естественно рассматривать каждую интернет-страницу как отдельный источник, поскольку она может иметь отличную от других веб-ресурсов точность. Можно даже определить источник как некоторый предикат на странице, что позволяет оценить ее достоверность относительно этого предиката. Однако при высокой детализации источников может возникнуть проблема «разреженности» данных, что затруднит адекватную оценку их точности. С другой стороны, существуют страницы, содержащие слишком много фактов даже при максимальной степени детализации, что может вызывать проблемы, связанные с вычислительной сложностью.

Чтобы эффективно решать подобные проблемы, мы предлагаем «в динамике» выбирать степень детализации источников. Для малосодержательных страниц можно «отступить» к более высокому уровню иерархии, что позволит «распределить статистическую значимость» между связанными документами. Слишком «тяжелые» страницы можно разбивать на множество более «легких», и оценивать их точность независимо друг от друга. При слиянии страниц цель заключается в повышении статистической значимости оценок без потери эффективности. При разделении цель заключается в повышении эффективности работы алгоритма при минимальных изменениях самих оценок.

Для большей точности можно определять источник на различных уровнях детализации, учитывая значения вектора свойств: (сайт, предикат, страница) в порядке от общего к частному. Можно построить иерархию таких источников. Например: (wiki.com) — родитель (wiki.com, дата рождения), который в свою очередь является родителем (wiki.com, дата рождения, wiki.com/page1.html). Определим два оператора:

Разделение (Split): При разделении «тяжелой» страницы она случайным образом разбивается на суб-страницы одинакового размера. Пусть W — источник размера |W|, а M — максимально допустимый размер. Равномерно распределим триплеты W в подможества , каждое из которых представляет суб-страницу. М устанавливается так, чтобы не требовалось избыточного количества разделений страниц и при этом не возникало проблем с вычислительной сложностью.

Слияние/Объединение (Merge): При слиянии мелких страниц объединяются только те источники, которые имеют общие черты, например, один и тот же предикат или принадлежность к одному сайту. Следовательно, слиянию подлежат только потомки одного и того же родителя в иерархии. m устанавливается так, чтобы не было избыточных слияний, при этом статистическая значимость всех страниц была достаточной.

ПРИМЕР 4.1. Рассмотрим три источника: (website1.com, дата рождения), (website1.com, место рождения), (website1.com, пол), каждый с двумя триплетами, чего недостаточно для оценки качества. Мы можем объединить их в родительский источник, удалив второе свойство (предикат). Тогда получаем страницу (website1.com) с размером 2*3 = 6 триплетов, который предоставляет больше данных для оценки качества.

Подчеркнем, что при слиянии мелких источников результат может не иметь желаемого размера, т.е. по-прежнему иметь недостаточную статистическую значимость. Или, наоборот, получившаяся страница может быть слишком «тяжелой», если объединяется слишком много мелких страниц. В результате, возможно, потребуется многократное слияние новых страниц либо их разделение. Данные процессы формализованы в алгоритме 2.

W обозначены исходные источники и W’ — конечный результат разделения и слияния. В начале алгоритма W содержит все источники с максимальной степенью детализации и W’ =0. Рассмотрим каждый . Если W слишком «тяжелый», используем РАЗДЕЛЕНИЕ, чтобы разбить его на множество источников более низкого уровня. РАЗДЕЛЕНИЕ гарантирует, что каждый новый источник будет иметь желаемый размер. Таким образом, добавляются новые элементы во множество W’. Если W слишком «легкий», переходим к его родителю. Если же он уже на вершине исходной иерархии, т.е. не имеет родителя, то добавляем его в W’, в противном случае к нему добавляется Wpar. Наконец источники с допустимым размером перемещаются непосредственно в W’.

ПРИМЕР 4.2. Рассмотрим множество из 1000 источников (W; P_i; URL_i) i=[1; 1000], т.е. они находятся на одном веб-сайте, у каждого свой предикат и уникальный URL. На выходе необходимо получить источники с размером [5; 500]. Тогда алгоритм MULTILAYERSM реализует три стадии.

На первой стадии каждый источник считается слишком маленьким и заменяется родителем (W; P_i). На второй стадии каждый новый источник по-прежнему считается слишком маленьким и снова заменяется родителем (W). На третьей стадии единственный оставшийся источник считается слишком большим, а потому равномерно разделяется на две суб-страницы. Алгоритм заканчивается с 2 источниками, каждый с размером 500.

В завершении раздела покажем, что данный метод применим и для экстракторов. Определим экстрактор, используя следующий вектор свойств (экстрактор, паттерн, предикат, сайт). Самая высокая степень детализации соответствует качеству определенного паттерна экстрактора (у различных паттернов может быть разное качество) для парсинга определенного предиката из определенного веб-сайта (у паттерна может быть различное качество на разных веб-сайтах).

5. РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ

В этом разделе представлены результаты наших экспериментов на синтетическом множестве данных (для которых известны истинные значения фактов) и на большом множестве реальных данных. Показано, что, во-первых, предлагаемый алгоритм может эффективно оценивать правильность парсинга, достоверность триплетов и точность страниц; во-вторых предлагаемая модель значительно превосходит современные методы синтеза знаний и, в-третьих, KBT предоставляет полезные дополнительные данные для оценивания качества веб-ресурсов.

5.1 Исходные данные для экспериментов

5.1.1 Метрики

Необходимо оценить, насколько хорошо модель определяет правильность парсинга, вероятность истинности триплета и точность страницы. Преимущество синтетических данных заключается в том, что известны основные характеристики страниц и фактов, а потому можно провести точное оценивание по всем трем направлениям. Используем квадратическую невязку в качестве метрики качества: чем ниже ее значение, тем лучше. Определим следующие метрики: SqV — среднеквадратическая невязка между  и истинным значением ; SqC — среднеквадратическая невязка между  и истинным значением ; и SqA — среднеквадратическая невязка между  и истинным значением .

Для реальных данных, однако, как будет показано ниже, у нас нет некоего стандарта для оценки достоверности источников, известны лишь оценки некоторых триплетов и правильности парсинга. Следовательно на реальных данных основной упор идет на измерение качества оценки истинности триплетов. В дополнение к SqV будем использовать еще 3 метрики с той же целью, с которой они применялись в [11].

• Взвешенное отклонение (WDev): WDev показывает, насколько точны оценки вероятностей. Разобьем множество триплетов согласно соответствующим вероятностям на подможества: [0; 0.01), …, [0.04; 0.05), [0.05; 0.1), …, [0.9; 0.95), [0.95; 0.96), …, [0.99; 1), [1, 1] (большинство триплетов попадают вв [0; 0.05) и [0.95; 1], что дает более высокую степень детализации). Для каждого подмножества вычисляем точность триплетов согласно известным оценкам, т.е. реальным вероятностям истинности фактов. WDev измеряет среднеквадратическую невязку между оцененными и реальными вероятностями, взвешенную количеством триплетов в каждом подмножестве. Чем меньше ее значение, тем лучше.
• Площадь фигуры, ограниченной кривой precision-recall (AUC-PR): AUC-PR определяет монотонность оценок вероятностей. Выстроим триплеты согласно расчитанным вероятностям и построим график PR-кривой, где по оси X откладываются значения recall, а по оси У — precision. AUC-PR равно площади фигуры, ограниченной полученной кривой: чем она больше, тем лучше.
• Покрытие (Cov): Cov показывает, для какой части триплетов вычисляется вероятность (как будет показано ниже, можно игнорировать данные страницы, качество которой не меняется от исходного значения на всех итерациях).

Подчеркнем, что на синтетических данных Cov=1 для всех методов, и сравнение различных технологий при помощи AUC-PR и WDev аналогично использованию SqV, поэтому далее мы пропустим данные оценки.

5.1.2 Сравниваемые методы

Мы сравниваем три основных метода. Первый — SINGLELAYER (однослойный) представляет современный метод синтеза знаний [11] (рассмотрен в Разделе 2). В частности, каждый источник описывается четверкой (экстрактор, веб-сайт, предикат, паттерн). Мы используем такой источник в синтезе знаний только в том случае, если его точность не остается на исходном значении при совершении итераций. Для данного метода устанавливается n = 100 и количество итераций, равное 5. Именно эти настройки, как показано в [11], давали наилучший результат.

Второй метод — MULTILAYER — представляет многослойную модель, описанную в Разделе 3. Чтобы получить рациональное время расчета, мы использовали самую высокую степень детализации, определенную в Разделе 4 для экстракторов и страниц. Каждый экстрактор представлен вектором (экстрактор, паттерн, предикат, веб-сайт), а каждый источник — вектором (веб-сайт, предикат, интернет-страница). При расчете правильности парсинга в качестве весов используется «уверенность», как в Разделе 3.5. Если экстрактор не вычисляет степень уверенности, то ее значение приравнивается к 1. При вычислении истинности триплетов по умолчанию мы используем улучшенную оценку p(C_wdv = 1|X), описанную в Разделе 3.3.3. Перерасчет априорных вероятностей p(C_wdv = 1) производится в соответствии с алгоритмом, представленным в Разделе 3.3.4, начиная с третьей итерации, так как вычисленные значения «стабилизируются» после второй итерации. Для зашумленных моделей устанавливаем n = 10 и γ= 0.25, однако наши исследования показали, что другие настройки приводят к схожим результатам. Исследование влияния изменения исходных параметров алгоритма на его результаты представлено в Разделе 5.3.3.

Третий метод — MULTILAYERSM представляет алгоритм SPLITANDMERGE в дополнение к многослойной модели, как описано в Разделе 4. По умолчанию устанавливаем минимальный и максимальный размер: m = 5 и M = 10K, эффект от их изменений будет рассмотрен в Разделе 5.3.4.

Каждый метод имеет еще две настройки. Первая определяет, какая версия p(X_ewdv|С_wdv) используется. Мы экспериментировали с ACCU и POPACCU. Оказалось, что работа однослойной модели на обоих версиях дает схожие результаты, но POPACCU незначительно лучше. При этом многослойная модель с использованием POPACCU показала худшие результаты по сравнению с ACCU-версией. Это объясняется тем, что нами еще не найден способ объединить модель POPACCU с улучшенной процедурой оценки, описанной в Разделе 3.3.3. Поэтому ниже будут представлены только результаты для версии ACCU.

Вторая настройка определяет то, каким образом задается качество источников. Можно назначить значения по умолчанию (А_w = 0.8; R_е = 0.8; Q_e = 0.2) или определить настройки на основе «золотого стандарта», как показано в Разделе 5.3. Для второго варианта добавим к названию метода +, чтобы отличать его от версии с настройками по умолчанию (например, SINGLELAYER +).

5.2 Эксперименты на синтетических данных

5.2.1 Исходные данные

Мы случайным образом сгенерировали множества данных, содержащие 10 источников и 5 экстракторов. На каждом источнике представлено 100 триплетов с точностью A= 0.7. Каждый экстрактор «извлекает» триплет из источника с вероятностью α = 0.5; для каждого источника он парсит существующий триплет с вероятностью R = 0.5; точность спарсенных субъектов (а также предикатов и объектов) P = 0.8 (другими словами, точность экстрактора — P_e = P³). В каждом эксперименте мы меняли один из параметров от 0.1 до 0.9 при зафискированных значениях других. Прогоны алгоритмов для каждого эксперимента повторялись 10 раз, а результаты усреднялись. Отметим, что настройка по умолчанию является сложным случаем, когда источники и экстракторы обладают довольно низким качеством.

5.2.2 Результаты эксперимента

На рисунке 3 представлены зависимости значений SqV, SqC и SqA от количества экстракторов. Метод SINGLELAYER учитывает все спарсенные триплеты при вычислении точности источников. Отметим, что многослойная модель при любых условиях дает лучший результат по сравнению с однослойной. При увеличении числа экстракторов для многослойной модели SqV довольно быстро убывает, SqC также убывает, хотя и с меньшей скоростью. Несмотря на то, что ввод дополнительных экстракторов увеличивает количество ложных парсингов, SqA практически не изменяется для MULTILAYER, при этом он заметно возрастает для SINGLELAYER.

Рисунок 3. Изменение метрик качества при увеличении числа экстракторов

Далее мы оценили качество экстракторов и источников. MULTILAYER по-прежнему показывает лучшее качество оценок по сравнению с SINGLELAYER при любых условиях, поэтому на рисунке 4 представлены только его результаты при изменении R, P и A. В целом, чем выше качество, тем меньше невязки, хотя наблюдаются незначительные отклонения от этой тенденции. При увеличении recall экстрактора (R) SqA не уменьшается, поскольку экстракторы увеличивают зашумление. При увеличении precision экстрактора (P) им оказывается слишком высокое доверие, а потому количество ложных триплетов увеличивается, и SqV незначительно возрастает. Аналогично при увеличении А несущественно возрастает SqA из-за роста количества ложных триплетов. Однако в целом мы считаем, что эксперименты на синтетических данных показали высокую эффективность алгоритма.

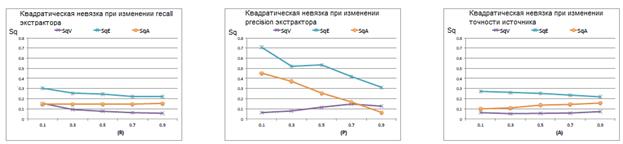
Рисунок 4. Изменение качества экстракторов и источников в зависимости от recall и precision экстракторов и точности источников.

5.3 Эксперименты на данных базы знаний

5.3.1 Исходные данные

Эксперименты проводились на основе триплетов, собранных в базе знаний [10] от 24/07/2014 (KV). В KV представлено 2.8 миллиарда триплетов, спарсенных из более чем 2-х миллиардов страниц 16-ю экстракторами на основе 40 миллионов паттернов. По сравнению со старой KV от 2/10/2013 [11] текущая коллекция на 75% больше, использует на 25% больше экстракторов и на 8% — паттернов, а также имеет вдвое больше интернет-страниц.

На рисунке 5 представлено распределение страниц и паттернов в зависимости от количества различных триплетов. С одной стороны наблюдаются огромные страницы: 26 URL, каждый из которых содержит 50K триплетов (такое число получается из-за ошибок парсинга), 15 веб-сайтов, каждый из которых содержит по 100M триплетов, и 43 паттерна, на основе каждого из которых парсится 1M триплетов. С другой стороны, имеются «длинные хвосты»: 74% URL, каждый из которых содержит менее 5 триплетов, и 48% паттернов, на основе каждого из которых парсится менее 5 триплетов. Именно для таких случаев создан алгоритм SPLITANDMERGE.

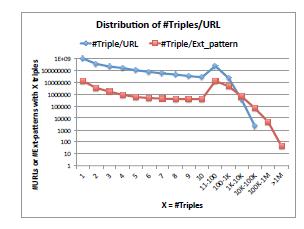
Рисунок 5. Распределение числа страниц и паттернов в зависимости от количества триплетов

Для определения истинности триплета мы используем два метода. Первый — Local-Closed World Assumption (LCWA) [10, 11, 15], который работает следующим образом. Триплет (s; p; o) считается верным, если он представлен в Freebase KB. Если триплет отсутствует в KB, но (s; p) существует с любым другим значением o’, то триплет (s; p; o) считается ложным. Оставшаяся часть триплетов (где (s; p) отсутствуют) считается неизвестной и удаляется из оценок. Таким образом мы смогли оценить достоверность 740 миллионов триплетов (26% из KV), 20% из которых верны (присутствуют во Freebase).

Во-вторых, мы используем проверку типа для определения неправильных парсингов. В частности мы считаем триплет (s; p; o) ложным, если 1) s = o; 2) тип s или o несовместим с типом, который определяется предикатом или 3) o вне ожидаемого диапазона (например, вес спортсмена составляет более чем 1000 фунтов). Было обнаружено 560 миллионов триплетов (20% в KV), которые не удовлетворяют данным условиям, т.е не являются ложными. По результатам применения обоих методов мы сформировали наш «золотой стандарт», включающий 1.3 миллиарда триплетов, 11.5% которых истинны.

5.3.2 Сравнительный анализ Singlelayer и Multilayer

В таблице 5 представлено сравнение результатов всех трех методов. На рисунке 8 – кривая точности оценок, а на рисунке 9 – кривая PR. Как видно, все методы имеют высокую точность, однако у многослойной модели наилучшая кривая PR. SINGLELAYER часто занижает вероятность для истинных триплетов и, как следствие, имеет много ложных отрицаний

Таблица 5. Сравнительный анализ различных методов

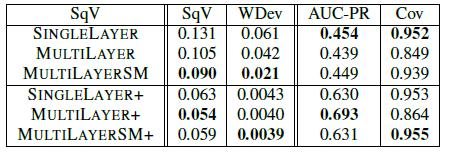
При этом у MULTILAYERSM лучшие результаты, чем у MULTILAYER, однако неожиданным стало то, что MULTILAYERSM+ работает хуже MULTILAYER+. Таким образом, можно сделать вывод о зависимости между степенью детализации источников и способом, которым мы определяем их точность.

Причины этого следующие. При начальной настройке источника и экстрактора на основе значений по умолчанию используется неконтролируемое обучение (неоцененные данные). В этом режиме MULTILAYERSM объединяет маленькие страницы так, чтобы лучше оценивать их качество, что дает преимущество перед MULTILAYER. Теперь рассмотрим случай с использованием «золотого стандарта». При этом мы, по существу, используем контролируемое обучение. Такая настройка значительно помогает при использовании высокой степени детализации источников и экстракторов, но при этом зачастую на выходе остается значительно меньше данных, что ухудшает результаты MULTILAYERSM.

Чтобы исследовать качество оценок правильности парсинга, построим распределение оценок ошибочных триплетов (в идеале оценка вероятности их появления должна быть равной 0) и правильных триплетов. На рисунке 6 представлены результаты MULTILAYER+. Отметим, что в случае ошибочных триплетов MULTILAYER+ оценивает вероятность ниже 0.1 для 80% из них и выше 0.7 только для 8%. И наоборот, для правильных триплетов из Freebase MULTILAYER+ оценивает вероятность ниже 0.1 для 26% из них и выше 0.7 – для 54%, доказывая эффективность нашей модели.

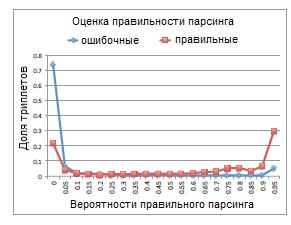
Рисунок 6. Оценка правильности парсинга

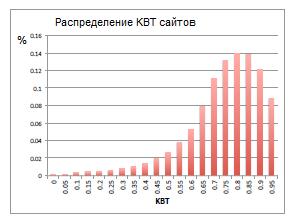
Рисунок 7. Распределение KBT сайтов с менее, чем 5 триплетами

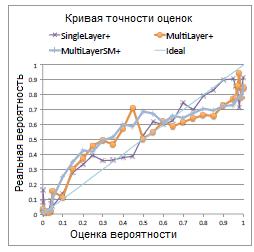
Рисунок 8. Кривая точности оценок

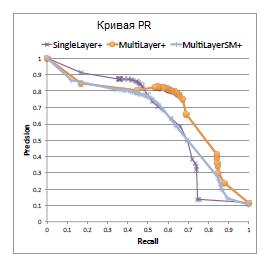
Рисунок 9.Кривая PR

5.3.3 Исследование последствий изменения алгоритма анализа.

В таблице 6 представлен эффект изменения различных «настроек» многослойного алгоритма анализа.

Таблица 6. Исследование влияния изменений алгоритма на результат

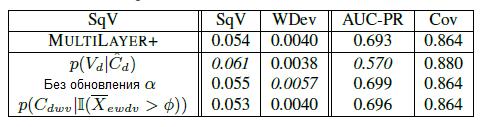
Строка  показывает, как изменяются результаты при использовании V_d (как описано в Разделе 3.3.2) вместо взвешивания на основе «уверенности» (Раздел 3.3.3). Как видно, метрика AUC-PR значительно снижается, а SqV возрастает. Т.е. отбрасывая погрешности C_d, мы оцениваем вероятность меньше 0.05 для правильности 93% триплетов.

Строка «без обновления α» показывает, как изменяются результаты при фиксированном  вместо использования схемы обновления, описанной в Разделе 3.3.4. Как видно, большинство метрик остается на прежнем уровне, однако WDev значительно увеличивается, что означает ухудшение точности оценок вероятностей.

Строка  показывает, как изменяются оценки при использовании пороговой обработки весов «уверенности» при границе отсечки φ = 0 вместо методики, описанной в Разделе 3.5. Как видно, пороговая отсечка дает немного лучший результат, что соответствует нашим наблюдениям для случаев, когда некоторые экстракторы неправильно оценивают свою «уверенность» [11].

5.3.4 Вычислительная эффективность

Все алгоритмы были реализованы во FlumeJava [6], которая предназначена для распределенных вычислений. Абсолютное время расчета существенно зависит от количества используемых машин. Поэтому в Таблице 7 показана только относительная эффективность алгоритмов. В ней представлены данные о: времени подготовки (Prep), включая разделение и объединение веб-источников и экстракторов; времени итераций (Iter), включая вычисление правильности парсинга (ExtCorr), истинности триплетов (TriplePr), точности источников (SrcAccu) и качества экстрактора (ExtQuality). Для каждой операции представлено среднее время выполнения по результатам 5 итераций. По умолчанию m = 5; M = 10K.

Таблица 7. Относительное время вычислений

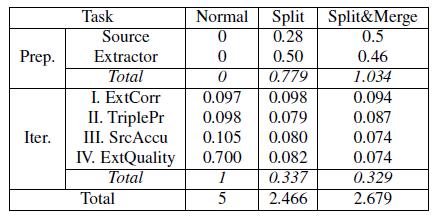
Во-первых, отметим, что разделение больших источников и экстракторов может значительно сократить время расчета. На нашем массиве данных некоторые экстракторы парсят огромное число триплетов. При разделении таких экстракторов скорость вычисления их качества возрастает на 8.8%. Кроме того, можно заметить, что разделение «тяжелых» страниц также уменьшает время вычисления их точности на 20%. В среднем скорость каждой итерации возрастает на 3%. Хотя для некоторых разделений общее время расчета сократилось наполовину.

Во-вторых, отметим, что слияние несущественно увеличивает время выполнения. Хотя скорость подготовки снижается на 33%, время выполнения каждой итерации снижается (на 2.4%), потому что уменьшается количество источников и экстракторов. Полное время выполнения увеличивается по сравнению с разделением на 8.6%. При этом подход, который использует самую грубую исходную степень детализации, а затем итеративно разделяет крупные источники и экстракторы, увеличивает время подготовки в 3.8 раза.

В завершение рассмотрим влияние изменения параметров m и M. Колебания М в пределах от 1K до 50K незначительно влияют на качество оценки, однако снижение значения до M = 1K (много разделений) замедляет подготовку на 19%, а увеличение до M = 50K (мало разделений) замедляет анализ на 21%, т.е. обе крайности увеличивают время расчета. С другой стороны, увеличение m до значений, превышающих 5, не влияет на работу алгоритма, в то время как снижение до m = 2 (меньше объединений) ухудшает WDev на 29% и анализ на 14%.

5.4 Исследование KBT

Исследуем, насколько хорошо наша модель оценивает достоверность интернет-страниц. Наш массив данных содержит более 2 миллиардов страниц (26 миллионов веб-сайтов). Среди них 119 миллионов страниц (5.6 миллионов сайтов), с которых, согласно многослойной модели, было спарсено более 5 триплетов. На рисунке 7 представлено распределение KBT для этих сайтов. Отметим, что мода (пик) распределения приходится на 0.8, при этом у 52% сайтов КВТ превышает 0.8.

5.4.1 Сравнение KBT с PageRank

Так как у нас нет информации об истинном качестве всех интернет-страниц, проведем сравнение модели с PageRank. Вычислим PageRank для всех страниц в сети, сведя полученные оценки к диапазону [0; 1]. На рисунке 10 представлены значения KBT и PageRank для 2000 случайно выбранных веб-сайтов. Как и ожидалось, данные характеристики практически ортогональны (независимы). Исследуем два случая, когда KBT значительно отличается от PageRank.

Малое значение PageRank и большое значение KBT (нижний правый угол графика): Чтобы понять, какие страницы получают высокий KBT, мы случайным образом выбрали 100 веб-сайтов, KBT которых выше 0.9. Число спарсенных триплетов от каждого из них варьируется от нескольких сотен до миллионов. С каждого сайта выделили 3 наиболее часто встречающихся предиката, а затем из них случайным образом выбрали 10 триплетов, вероятность истинности которых превышает 0.8. Далее была произведена ручная оценка данных сайтов, согласно следующим 4 критериям:

• Правильность триплетов: по крайней мере 9 фактов верны.
• Правильность парсинга: по крайней мере 9 триплетов спарсены правильно (т.е. мы можем оценить достоверность сайта без учета ошибок парсинга).
• Релевантность темы: мы определяем главные темы для сайта, согласно его названию и информации на странице «О нас». Затем определяется, существует ли, по крайней мере, 9 триплетов, релевантных выделенным темам (например, если сайт о бизнес-каталогах в Южной Америке, то триплеты о городах и странах в ЮА считаются нерелевантными).
• Нетривиальность: хотя бы часть триплетов являются нетривиальными (например, если наиболее часто встречающийся триплет веб-сайта об индийском кино гласит, что язык фильма — индийский, то считается, что он тривиальный).

Считаем сайт заслуживающим доверия, если он удовлетворяет всем четырем критериям. Среди выделенных 100 веб-сайтов 85 считаются достоверными. Среди остальных: 2 – тематически нерелевантные, 12 – содержат слишком мало нетривиальных триплетов, 2 – имеют более одной ошибки парсинга (у одного веб-сайта – 2 ошибки). Однако только у 20 из этих 85 сайтов PageRank превышает 0.5. Это говорит о том, что КВТ может считать сайты заслуживающими доверия, даже если они имеют малое значение PageRank.

Большое значение PageRank и низкое значение KBT (верхний левый угол графика): Рассмотрим 15 веб-сайтов со сплетнями, которые перечислены в [16]. 14 из них имеют высокий PageRank и относятся по данному параметру к 15% лучших сайтов в сети, т.к. такие ресурсы, как правило, очень популярны. Однако каждый из них имеет KBT, находящийся в нижней половине, т.е. считается, что они заслуживают меньше доверия, чем половина всех веб-сайтов. Еще один пример сайтов с высоким PageRank и низким КВТ — форумы. Например, на answers.yahoo.com содержится триплет “Кэтрин Зета-Джонс из Новой Зеландии”, хотя, согласно Википедии, она родилась в Уэльсе.

5.4.2 Перспективы метода

Хотя было показано, что КВТ предоставляет полезную информацию о достоверности, которая независима от традиционных характеристик сайта, таких, как PageRank, в наших исследованиях мы наметили направления для дальнейшего совершенствования модели:

1. Чтобы избегать KBT-оценок триплетов, не релевантных относительно тематики, необходимо определять главные темы веб-сайта и фильтровать триплеты, сущности или предикаты которых не соответствуют им.

2. Чтобы избегать KBT-оценок тривиальных триплетов, необходимо определять, тривиальна ли информация, содержащаяся в триплете. Один из вариантов решения этой задачи заключается в том, чтобы считать предикат с очень низким разнообразием объектов менее информативным. Другой вариант заключается в использовании IDF триплета так, что факт с малой IDF получает меньший вес при расчете KBT.

3. Наши экстракторы (и большинство современных экстракторов) по-прежнему имеют ограниченные возможности, которые не позволяют определить KBT для всех веб-сайтов. В наших планах увеличение покрытия KBT путем расширения метода до технологий, работающих по схеме открытого IE (information extraction — парсинга информации), выходящих за рамки структур, описанных [14]. Стоит отметить, что хотя данные методы способны спарсить больше триплетов, они могут увеличить зашумление данных.

4. Некоторые веб-сайты заимствуют данные с других источников. Определение таких ресурсов требует использования специальных методик, таких, как идентификация копирования. Применение технологий, подобных [7, 8], было опробовано в [23], но требуется больше исследований, прежде чем данные методы можно будет использовать для анализа спарсенных из миллиардов веб-источников данных.

6. СВЯЗАННЫЕ ИССЛЕДОВАНИЯ

Существует множество исследований, посвященных изучению проблемы оценки качества веб-страниц. PageRank [4] и анализ авторитетности источника [19] строят характеристики на основе анализа ссылок [3]. EigenTrust [18] и TrustMe [28] исследуют характеристики поведения источника в сети P2P. Web topology [5], TrustRank [17] и AntiTrust [20] отслеживают веб-спам. Достоверность, основанная на базе знаний, которую мы рассматриваем в данной статье, отличается от всех этих подходов, т.к. она отображает важную внутреннюю характеристику страницы — правильность фактической информации, которую она содержит.

Наше исследование относится к работам, посвященным синтезу данных [1, 12, 23], основная цель которых заключается в разрешении противоречий между данными, полученными из различных источников, и определении фактов, которые имеют отношение к реальности. Большая часть последних работ в этой области рассматривает достоверность источников, оцененную на основе ссылочных методов [24, 25], методов информационного поиска [29], точностных методов [8, 9, 13, 21, 27, 30] и методов анализа графов [26, 31, 33, 32]. Однако данные технологии не используют понятие экстрактора и, следовательно, не могут различать надежные и ненадежные источники.

Графовые модели были предложены, чтобы решить задачу синтеза данных [26, 31, 32, 33]. Они схожи с нашей однослойной моделью, представленной в Разделе 2.2. В частности, [26] использует принцип единственности истинного значения, [32] – числовые значения, [33] допускает несколько истинных значений и [31] использует связи между страницами. Однако данные подходы не рассматривают понятие экстрактора и, следовательно, не учитывают тот факт, что источники и экстракторы вносят качественно различные виды шума. Кроме того, массивы данных, используемые в их экспериментах, как правило, на 5-6 порядков меньше наших, и используемые ими алгоритмы значительно медленнее нашего. Использование многослойной модели и объем наших экспериментальных данных выделяют наше исследование из других работ, посвященных синтезу данных.

В завершении отметим, что самая близкая к данной — наша работа, посвященная синтезу знаний [11]. Их подробное теоретическое сравнение было произведено в Разделе 2.3, а в Разделе 5 было представлено экспериментальное сравнение, которое показало, что MULTILAYER превосходит SINGLELAYER с точки зрения синтеза знаний, кроме того, на его основе можно оценивать KBT-качество веб-ресурсов.

7. ЗАКЛЮЧЕНИЕ

В данной работе предлагается новая метрика для оценки качества веб-ресурсов – достоверность, основанная на базе знаний. Нами была предложена сложная вероятностная модель, которая совокупно оценивает корректность парсинга, достоверность фактов и точность источников. Кроме того, мы представили алгоритм, который позволяет в динамике менять степень детализации для каждой страницы.

Экспериментальные исследования показали высокую эффективность метода в области оценки качества веб-страниц, а также его превосходство по сравнению с существующими технологиями синтеза знаний.

8. ССЫЛКИ

[1] J. Bleiholder and F. Naumann. Data fusion. ACM Computing Surveys, 41(1):1–41, 2008.

[2] K. Bollacker, C. Evans, P. Paritosh, T. Sturge, and J. Taylor. Freebase: a collaboratively created graph database for structuring human knowledge. In SIGMOD, pages 1247–1250, 2008.

[3] A. Borodin, G. Roberts, J. Rosenthal, and P. Tsaparas. Link analysis ranking: algorithms, theory, and experiments. TOIT, 5:231–297,2005.

[4] S. Brin and L. Page. The anatomy of a large-scale hypertextual Web search engine. Computer Networks and ISDN Systems, 30(1–7):107–117, 1998.

[5] C. Castillo, D. Donato, A. Gionis, V. Murdock, and F. Silvestri. Know your neighbors: Web spam detection using the web topology. In SIGIR, 2007.

[6] C. Chambers, A. Raniwala, F. Perry, S. Adams, R. R. Henry, R. Bradshaw, and N. Weizenbaum. Flumejava: Easy, efcient data-parallel pipelines. In PLDI, pages 363–375, 2010.

[7] X. L. Dong, L. Berti-Equille, Y. Hu, and D. Srivastava. Global detection of complex copying relationships between sources. PVLDB, 2010.

[8] X. L. Dong, L. Berti-Equille, and D. Srivastava. Integrating conflicting data: the role of source dependence. PVLDB, 2(1), 2009.

[9] X. L. Dong, L. Berti-Equille, and D. Srivastava. Truth discovery and copying detection in a dynamic world. PVLDB, 2(1), 2009.

[10] X. L. Dong, E. Gabrilovich, G. Heitz, W. Horn, N. Lao, K. Murphy, T. Strohmann, S. Sun, and W. Zhang. Knowledge vault: A web-scale approach to probabilistic knowledge fusion. In IGKDD, 2014.

[11] X. L. Dong, E. Gabrilovich, G. Heitz, W. Horn, K. Murphy, S. Sun, and W. Zhang. From data fusion to knowledge fusion. PVLDB, 2014.

[12] X. L. Dong and F. Naumann. Data fusion–resolving data conflicts for integration. PVLDB, 2009.

[13] X. L. Dong, B. Saha, and D. Srivastava. Less is more: Selecting sources wisely for integration. PVLDB, 6, 2013.

[14] O. Etzioni, A. Fader, J. Christensen, S. Soderland, and Mausam. Open information extraction: the second generation. In IJCAI, 2011.

[15] L. A. Gal´arraga, C. Teflioudi, K. Hose, and F. Suchanek. Amie: association rule mining under incomplete evidence in ontological knowledge bases. In WWW, pages 413–422, 2013.

[16] Top 15 most popular celebrity gossip websites. https://www.ebizmba.com/articles/gossip-websites, 2014.

[17] Z. Gyngyi, H. Garcia-Molina, and J. Pedersen. Combating web spam with TrustRank. In VLDB, pages 576–587, 2014.

[18] S. Kamvar, M. Schlosser, and H. Garcia-Molina. The Eigentrust algorithm for reputation management in P2P networks. In WWW, 2003.

[19] J. M. Kleinberg. Authoritative sources in a hyperlinked environment. In SODA, 1998.

[20] V. Krishnan and R. Raj. Web spam detection with anti-trust rank. In AIRWeb, 2006.

[21] Q. Li, Y. Li, J. Gao, B. Zhao, W. Fan, and J. Han. Resolving conflicts in heterogeneous data by truth discovery and source reliability estimation. In SIGMOD, pages 1187–1198, 2014.

[22] X. Li, X. L. Dong, K. B. Lyons, W. Meng, and D. Srivastava. Truth finding on the DeepWeb: Is the problem solved? PVLDB, 6(2), 2013.

[23] X. Li, X. L. Dong, K. B. Lyons, W. Meng, and D. Srivastava. Scaling up copy detection. In ICDE, 2015.

[24] J. Pasternack and D. Roth. Knowing what to believe (when you already know something). In COLING, pages 877–885, 2010.

[25] J. Pasternack and D. Roth. Making better informed trust decisions with generalized fact-finding. In IJCAI, pages 2324–2329, 2011.

[26] J. Pasternack and D. Roth. Latent credibility analysis. In WWW, 2013.

[27] R. Pochampally, A. D. Sarma, X. L. Dong, A. Meliou, and D. Srivastava. Fusing data with correlations. In Sigmod, 2014.

[28] A. Singh and L. Liu. TrustMe: anonymous management of trust relationshiops in decentralized P2P systems. In IEEE Intl. Conf. on Peer-to-Peer Computing, 2003.

[29] M. Wu and A. Marian. Corroborating answers from multiple web sources. In Proc. of the WebDB Workshop, 2007.

[30] X. Yin, J. Han, and P. S. Yu. Truth discovery with multiple conflicting information providers on the web. In Proc. of SIGKDD, 2007.

[31] X. Yin and W. Tan. Semi-supervised truth discovery. In WWW, pages 217–226, 2011.

[32] B. Zhao and J. Han. A probabilistic model for estimating real-valued truth from conflicting sources. In QDB, 2012.

[33] B. Zhao, B. I. P. Rubinstein, J. Gemmell, and J. Han. A Bayesian approach to discovering truth from conflicting sources for data integration. PVLDB, 5(6):550–561, 2012.